Riding the Angle Bisector
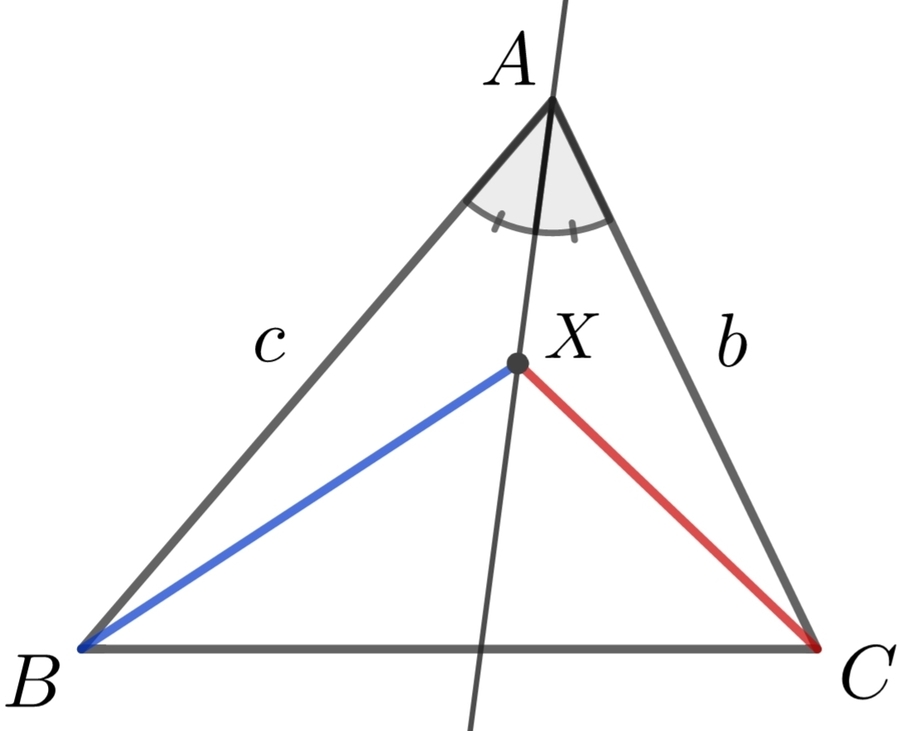
Consider a with a point that lies on the angle bisector of .
Let and be the minimum and maximum values of the ratio .
Find .
Note: and are the sides opposite to the and respectively.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Drop perpendiculars from X to sides A B and A C at P and Q respectively:
Then A P X Q is a kite, with A P = A Q = t (say) and P X = Q X = t tan 2 A .
Also, B P = c − t and C Q = b − t .
By Pythagoras, B X 2 = ( c − t ) 2 + t 2 tan 2 2 A = k 2 t 2 − 2 c t + c 2
where k = sec 2 A , and similarly
C X 2 = k 2 t 2 − 2 b t + b 2
We are interested in the max/min values of f ( t ) = k 2 t 2 − 2 b t + b 2 k 2 t 2 − 2 c t + c 2
Setting f ′ ( t ) = 0 and tidying up, we find at the max/min, t 2 − ( b + c ) t + k 2 b c = 0
After solving and substituting, and some messy algebra, we find M m = b c .
I suspect there's a better approach once f ( t ) is found - the function is not complicated, and nor is the final result; calculus is probably not the best method.