Riding The Sinusoid
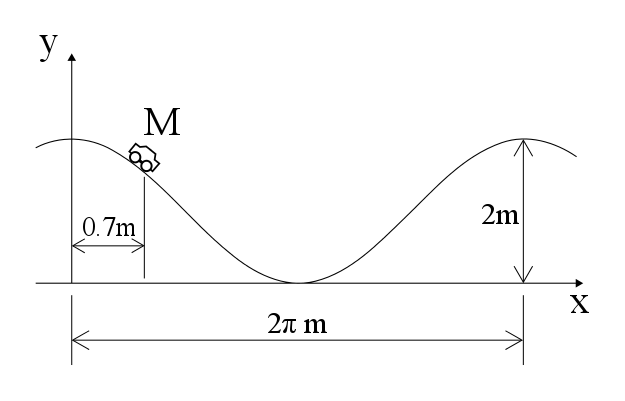
There is a point mass on a sinusoid path. The height of the curve is described by the equation where . The initial position of the point is and starts moving from rest.
Find the period of the motion in seconds to the nearest integer.
Details and Assumptions :
- Take .
There is no friction between the body and the surface.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Because there is no friction we can write the conservation of energy and find the velocity of the body at any point given as follows: m g y 0 = 2 1 m v 2 + m g y ( x ) v = 2 g ( y 0 − y ( x ) ) But v = d t d s where d s is the arc element of the curve. In our case: d s = 1 + y ′ 2 ( x ) d x Substituting in the formula for v we get: d t d x 1 + y ′ 2 ( x ) = 2 g ( y 0 − y ( x ) ) Rearranging: d t = 2 g ( y 0 − y ( x ) ) 1 + y ′ 2 ( x ) d x Now we will integrate only on a half of the motion and then we will multiply our result by 2: 0 ∫ T d t = 0 . 7 ∫ 2 π − 0 . 7 2 0 ( cos ( 0 . 7 ) − cos ( x ) ) 1 + sin 2 ( x ) d x T = 2 . 0 0 1 8 4 So the final result is P = 2 T = 4 . 0 0 3 6 s