Right Angle Quarter Circle
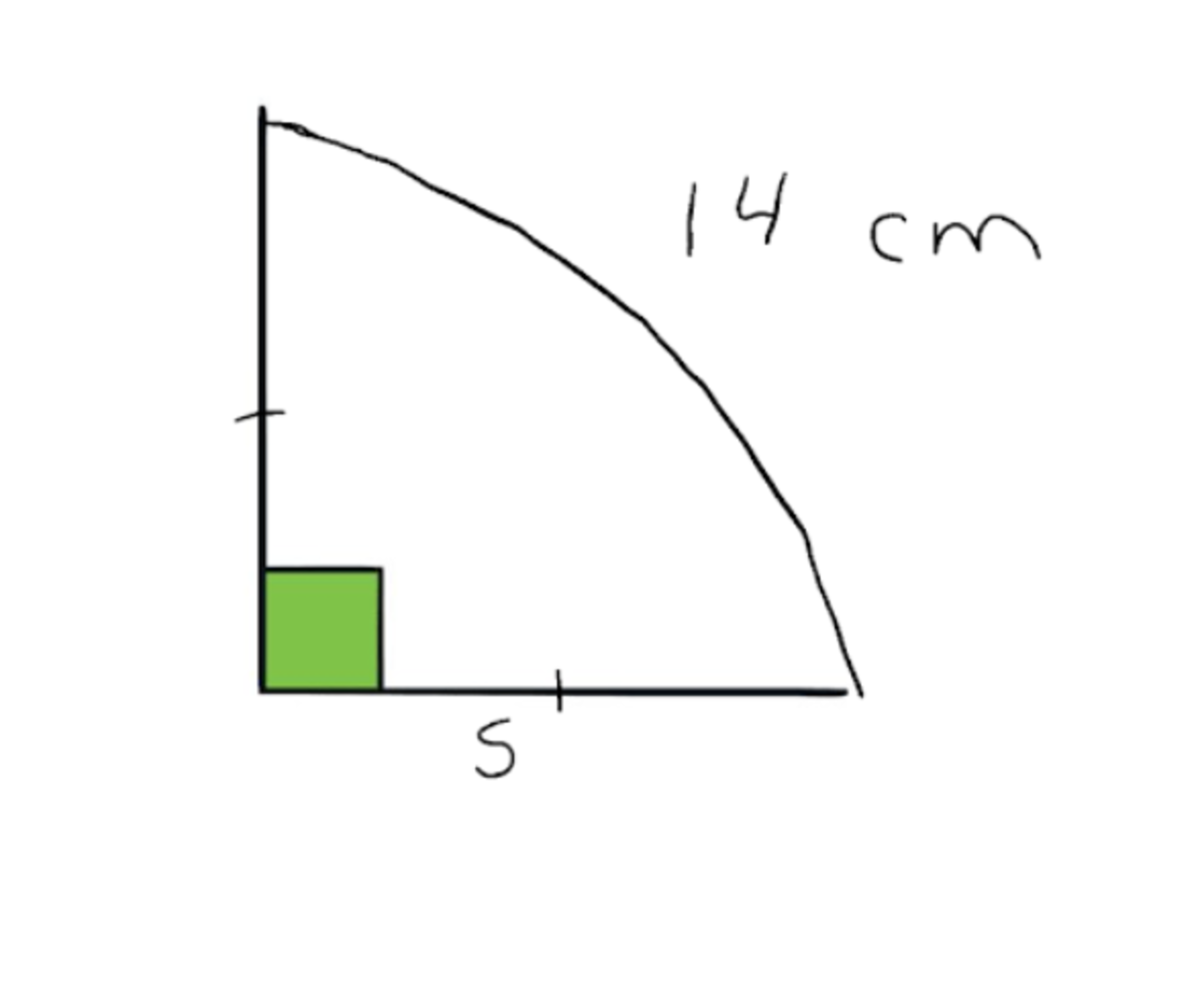 Solve for "s". Feel free to use a calutator.
Solve for "s". Feel free to use a calutator.
Round to the nearest whole number.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Imagine 3 other figures connected by the straght sides all togeter to form a circle (my apologies if the quarter-circle isn't perfect: I drew it myself freehanded). When you imagine this, you will see that the arc connecting the two striaght lines (obviously not where the to lines meet to form the right angle) is 4 1 of the total circumference of the circle.
C = 1 4 ∗ 4 = 5 6 c m
But this isn't what the question is asking. We need the diameter of the circle, and then divide it by 2 to find the value of s ( s = radius of the circle). We can find the diameter from a circumference by rearranging the formula C = πd:
C = π d
When we divide each side by π, we get:
π C = d
Now lets plug in the numbers:
3 . 1 4 1 5 5 6 = d
Now divide by 2:
2 1 7 . 8 2 5 8 7 9 3 6 = 8 . 9 1 2 9 3 9 6 7 8
Finally, round to the nearest integer:
8 . 9 1 2 9 3 9 6 7 8 ≈ 9
Formula for arc length: s = r θ where θ is the central angle in radians, r is the radius of the sector and s is the arc length.
We can form the equation r ⋅ θ 2 π = s 1 4 which can be solved by multiplying by π 2 :
r = π 2 8 = 8 . 9 1 2 6 7 6 8 ⋯ ≈ 9 (nearest whole number)