Right-angled triangle
△
A
B
C
is a right-angled triangle, where
A
C
=
3
and
B
C
=
4
. Let
P
be a point on the hypotenuse of the triangle. We drop perpendiculars from
P
to
A
C
and
B
C
, the footpoints of which are
X
and
Y
.
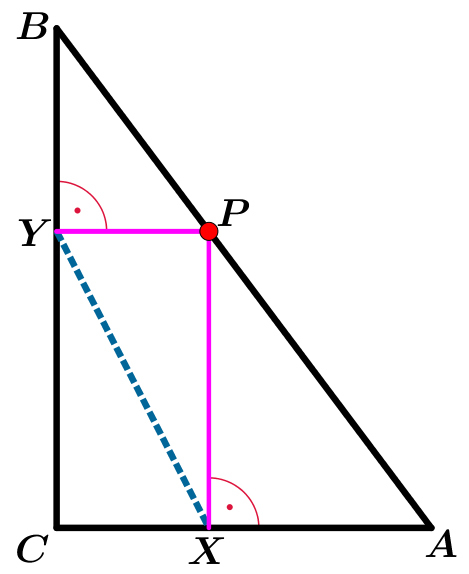
If the minimum value of X Y is n m , where m and n are coprime integers, then find the value of m + n .
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let C X = x and P X = y . Then, we have:
X Y = x 2 + y 2 = x 2 + 9 1 6 ( 3 − x ) 2 = 9 2 5 x 2 − 9 6 x + 1 4 4 = 9 2 5 ( x 2 − 2 5 9 6 x + ( 5 0 9 6 ) 2 − ( 5 0 9 6 ) 2 + 2 5 1 4 4 ) = 9 2 5 ( ( x − 5 0 9 6 ) 2 + 2 5 2 1 2 9 6 ) Note that y = 3 4 ( 3 − x ) Note that ( x − 5 0 9 6 ) 2 ≥ 0
⟹ min ( X Y ) = 9 2 5 ( 0 + 2 5 2 1 2 9 6 ) = 5 1 2
⟹ m + n = 1 2 + 5 = 1 7
Let X C = a , Y C = X P = b hence X B = 4 − a Now observe XBP is similar to CBA so we have b 4 − a = 3 4 → 1 2 = 4 b + 3 a . Now we wish to minimze a 2 + b 2 which is equivalent to minimizing the distance from the origin to the line 1 2 = 4 b + 3 a . Hence we take the perpendicular distance which is trivially 5 1 2 1 7
Clearly, YX = CP. We need to locate point P on the hypotenuse so that CP is perpendicular to BA. The slope of BA is -4/3. we want the slope of CP to be 3/4, so that the product of slopes = -1. Then if (x,y) are the coordinates of P, we have ,y = (3/4)x, and (CP)^2 = x^2 + (3x/4)^2, so CP = (5/4)x. We have: (3/4)x/(3 - x) = 4/3, or x = 48/25. then CP = (5/4)*(48/25) = 12/5, and the sum = 17. Ed Gray
Since ∠ A C B = 9 0 ° , the C X P Y quadrilateral is a rectangle, so X Y = C P . So we need to find the minimum value of C P . It's clear that it becomes the least when ∠ C P A = 9 0 ° , ie C P is a perpendicular. So imagine that now X Y is the least. Here the area of the triangle is: A C ∗ B C = 3 ∗ 4 = 1 2 = C P ∗ A B = 3 2 + 4 2 ∗ C P = 5 C P From that min ( C P ) = 5 1 2 .
Therefore the answer is 1 7 .