Right is right
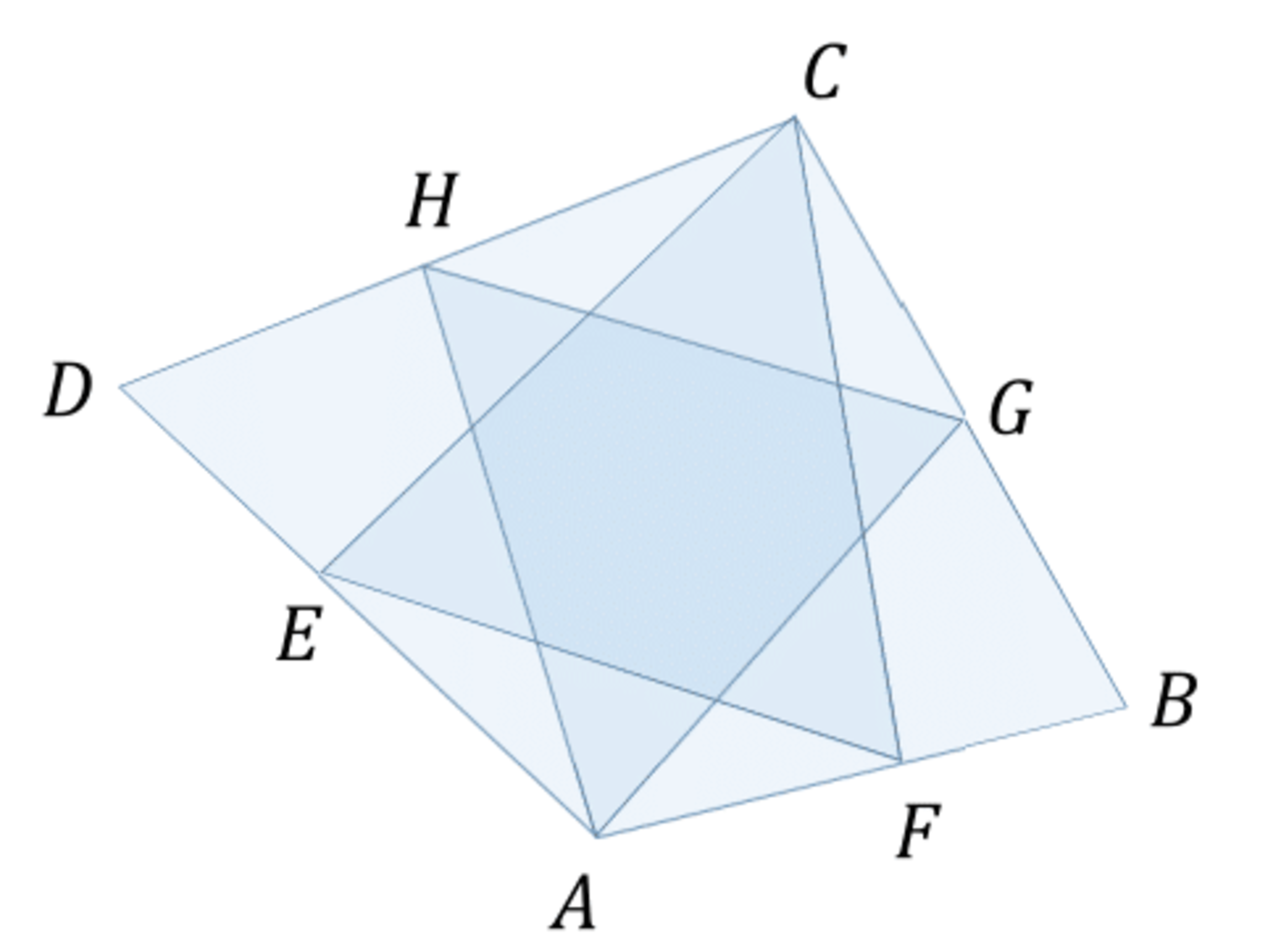
Two right isosceles triangles are inscribed in a quadrilateral. Their right angles are at opposing vertices of the quadrilateral. Their other vertices are midpoint of its sides. Find the largest angle of the quadrilateral.
Details: A F = F B , B G = G C , C H = H D , D E = E A
∠ E C F = 9 0 ∘ , ∠ H A G = 9 0 ∘ , A H = A G , C E = C F
Drawing is not to scale.
Inspiration: Just one step to regularity of quadrilateral by Rohit Camfar.
The answer is 143.13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
L
e
f
t
u
p
o
n
t
h
e
r
e
a
d
e
r
t
o
p
r
o
v
e
t
h
a
t
A
B
C
D
i
s
a
r
h
o
m
b
u
s
.
Little CONSTRUCTION.
From the statement of the problem, it is not immediately known that DB=GH. That is part of what needs to be shown to be true.
Log in to reply
Actually, DB is not equal to GH. It is twice. I have used fact that DB || GH. That is obvious through Midpoint theorem.The only thing which I have escaped is to prove that ABCD is a rhombus, which is very obvious in this situatiob and can be proved through congruency.
Log in to reply
Thanks for straightening me out. Now I can see it.
I meant to say parallel, sorry. DB parallel to GH.
Its unnecessarily confusing to make the drawing intentionally incorrect.
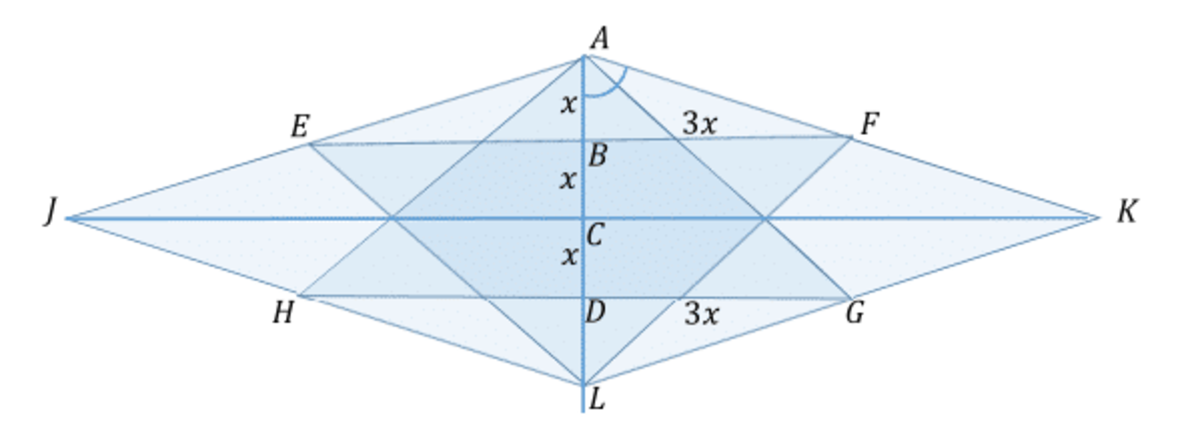We can see that
A
B
=
B
C
=
C
D
. The first equality comes from the fact that
E
and
F
are midpoints of
A
J
and
A
K
, the second from symmetry between triangles
A
H
G
and
L
E
F
.
The entire length of A D = D G = B F . The first equality is from the position of the two segments in the right isosceles triangle A H G , the other from the same symmetry as before.
So in the triangle A B F the angle B A F = a r c t a n ( x 3 x ) = a r c t a n 3 = 7 1 . 5 6 5 ∘ , giving us the angle J A K = 2 × 7 1 . 5 6 5 ∘ = 1 4 3 . 1 3 ∘ . .