Right Isosceles

Geometry Level 4

Given an isosceles right triangle A B C ABC , such that:

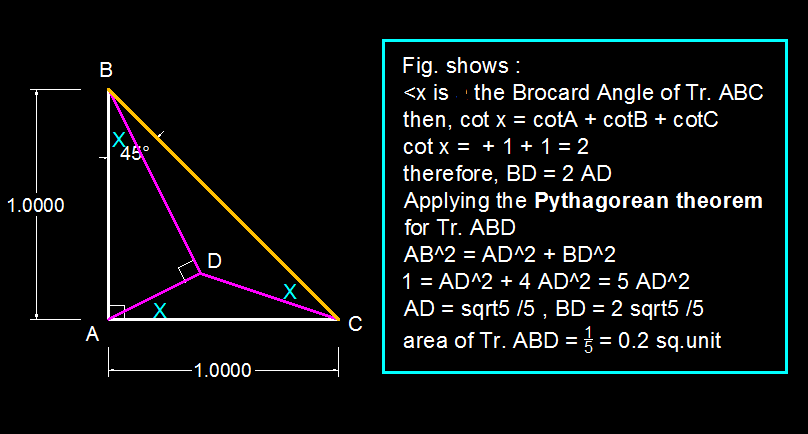
A B = A C = 1 , ∠ B A C = π 2 {AB=AC=1, \quad \angle BAC = \dfrac{\pi}2}

Let D D be a point inside the triangle such that:

∠ A D B = π 2 , ∠ A B D = ∠ B C D {\angle ADB = \dfrac{\pi}2, \quad \angle ABD = \angle BCD}

Find the area of △ A B D \triangle ABD .


The answer is 0.2.

Satyajit Mohanty by Satyajit Mohanty , 24, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

5 solutions

Ahmad Saad
Nov 7, 2015

8 Helpful 0 Interesting 0 Brilliant 0 Confused

did this question looked like level 4?

Department 8 - 5 years, 7 months ago

This looks amazing! Which software did you use? Does this also support LaTeX?

Alisa Meier - 5 years, 7 months ago

Log in to reply

Sorry for delaying my reply. The software is AuotoCad for engineers. You can get it from Internet sites or any engineer especially works as a consultant . Note that this software didn't support LaTex.

Ahmad Saad - 4 years, 6 months ago
Lu Chee Ket
Nov 6, 2015

Visualize triangle B D C of ( 4 5 ∘ − θ ) (45^\circ - \theta) , 13 5 ∘ 135^\circ and θ \theta .

Let B D be a a and by Sine rule,

2 s i n 13 5 ∘ = a s i n θ ⇒ s i n θ = a s i n 13 5 ∘ 2 = 0.5 a \frac{\sqrt{2}}{sin 135^\circ} = \frac{a}{sin \theta} \Rightarrow sin \theta = \frac{a sin 135^\circ}{\sqrt{2}} = 0.5 a

c o s θ = a cos \theta = a

T h e r e f o r e , t a n θ = 1 2 ⇒ s i n 2 θ = 2 t 1 + t 2 = 0.8 , Therefore, tan \theta = \frac{1}{2} \Rightarrow sin 2 \theta = \frac{2 t}{1 + t^2} = 0.8, where t = t a n θ t = tan \theta

Area of triangle = 1 2 a b s i n θ = 1 2 1 c o s θ s i n θ = 1 4 s i n 2 θ = 0.2 \frac {1}{2} a b sin \theta = \frac{1}{2} 1 cos \theta sin \theta = \frac{1}{4} sin 2 \theta = 0.2

A n s w e r : 0.2 Answer: 0.2

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0.2 + 0.2 + 0.1 = 0.5

The two triangles of 13 5 ∘ 135^\circ are of area 0.2 and 0.1 respectively.

Lu Chee Ket - 5 years, 7 months ago

Easy. We can consider B as(0,1) ; C as(1,0) ;A as(0,0); D as(h,k). Then applying slope eqns we get k-k^2=h and another eqn 2h=1-k. Now solving we get the point(0.4,0.2). Now from ADB we easily get area=0.2units.

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Reetun Maiti
Dec 3, 2015

Dead easy problem, just similar triangles, Triangles ADC and BDC are similar. Get relation between BD and DC. Then apply cosine Rule in triangle BDC. Get value of BD(and all other segments). Problem over

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Using the sketch by Ahmad Saad, Aplying the Sin law To triangles ADC and BDC, I n Δ A D C , S u m o f i n t e r n a l a n g l e s = 45 , ∴ ∠ A D C = 135 , S i m i l a r l y ∠ B D C = 135. A C ∗ S i n X S i n 135 = D C = B C ∗ S i n ( 45 − X ) S i n 135 . 1 ∗ S i n X ∗ 2 = 2 ∗ ( C o s X 2 − S i n X 2 ) . 1 = C o t X − 1. ∴ X = A r c t a n 0.5. A r e a Δ A B D = . 5 ∗ . 5 ∗ S i n 2 X = . 2 \\ In ~\Delta~ADC, ~Sum~ of~ internal~ angles~ =~45, \therefore~\angle ADC=135,~ Similarly~\angle BDC=135.\\ \dfrac{AC*SinX}{Sin135}=DC=\dfrac{BC*Sin(45-X)}{Sin135}.\\ 1*SinX*\sqrt2=\sqrt2*(\frac{CosX}{\sqrt2}-\frac{SinX}{\sqrt2}).\\ 1=CotX - 1. ~~~\therefore X=Arctan0.5.\\ Area \Delta~ABD=.5*.5*Sin2X=\Large~~~~\color{#D61F06}{.2}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...