Right or Wrong?
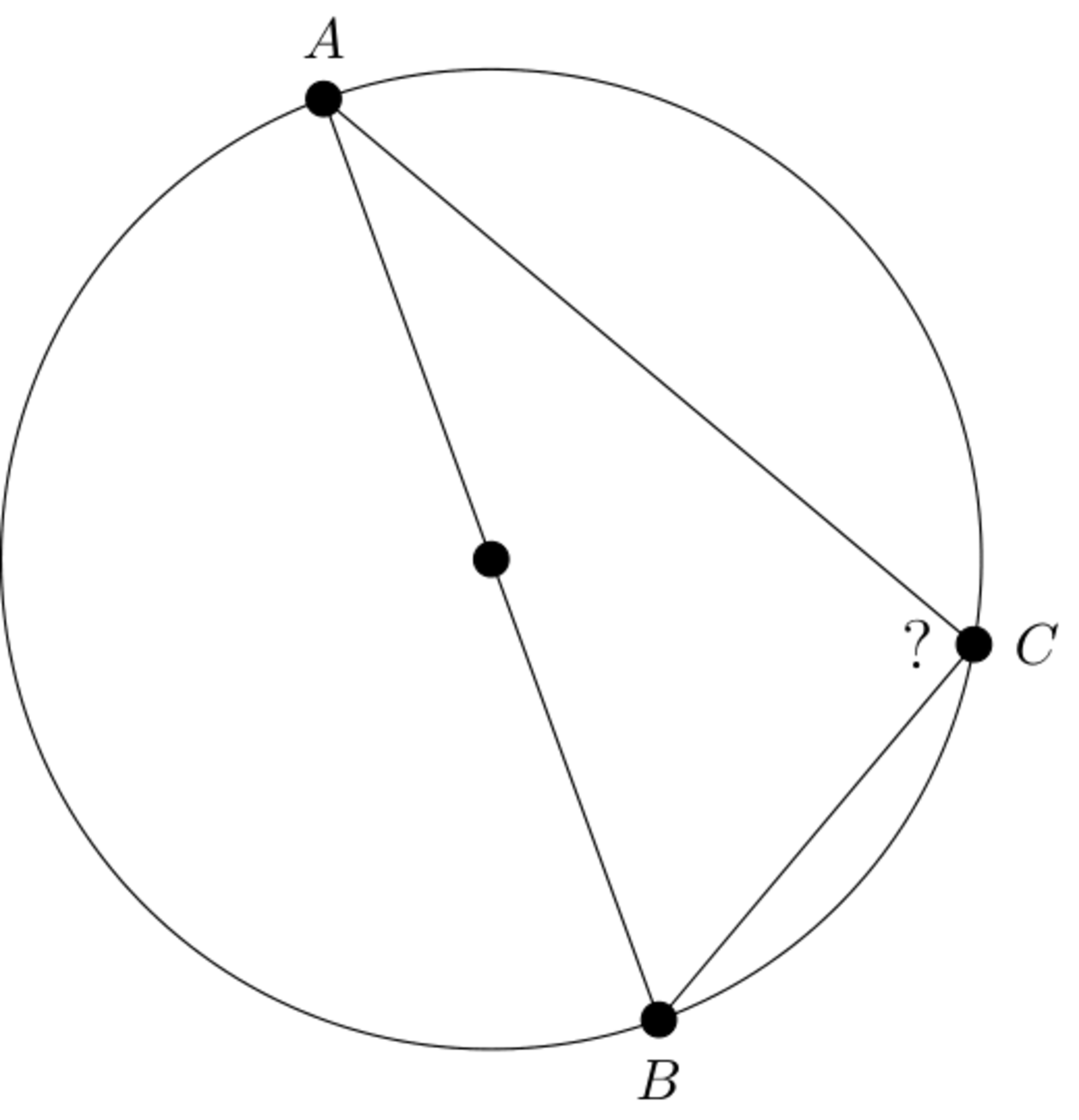
If the line segment is a diameter of the circle and is chosen uniformly at random on the circle, what is the probability that is a right angle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This is Thales' theorem. If you construct a line segment from the center to point C, you will construct two isoceles triangles. if we call the center D, ACD and DCB are the two triangles. Angles DAC and ACD are congruent. DCB and DBC are also congruent respectively. So DAC+ACD = 2DAC and DCB+DBC = 2DCB, then 2DAC+2DBC = 180. If we divide by two, DAC+DBC = 90 degrees. Therefore, there is 100% chance the angle will be 90 degrees.