Right Square Pyramids
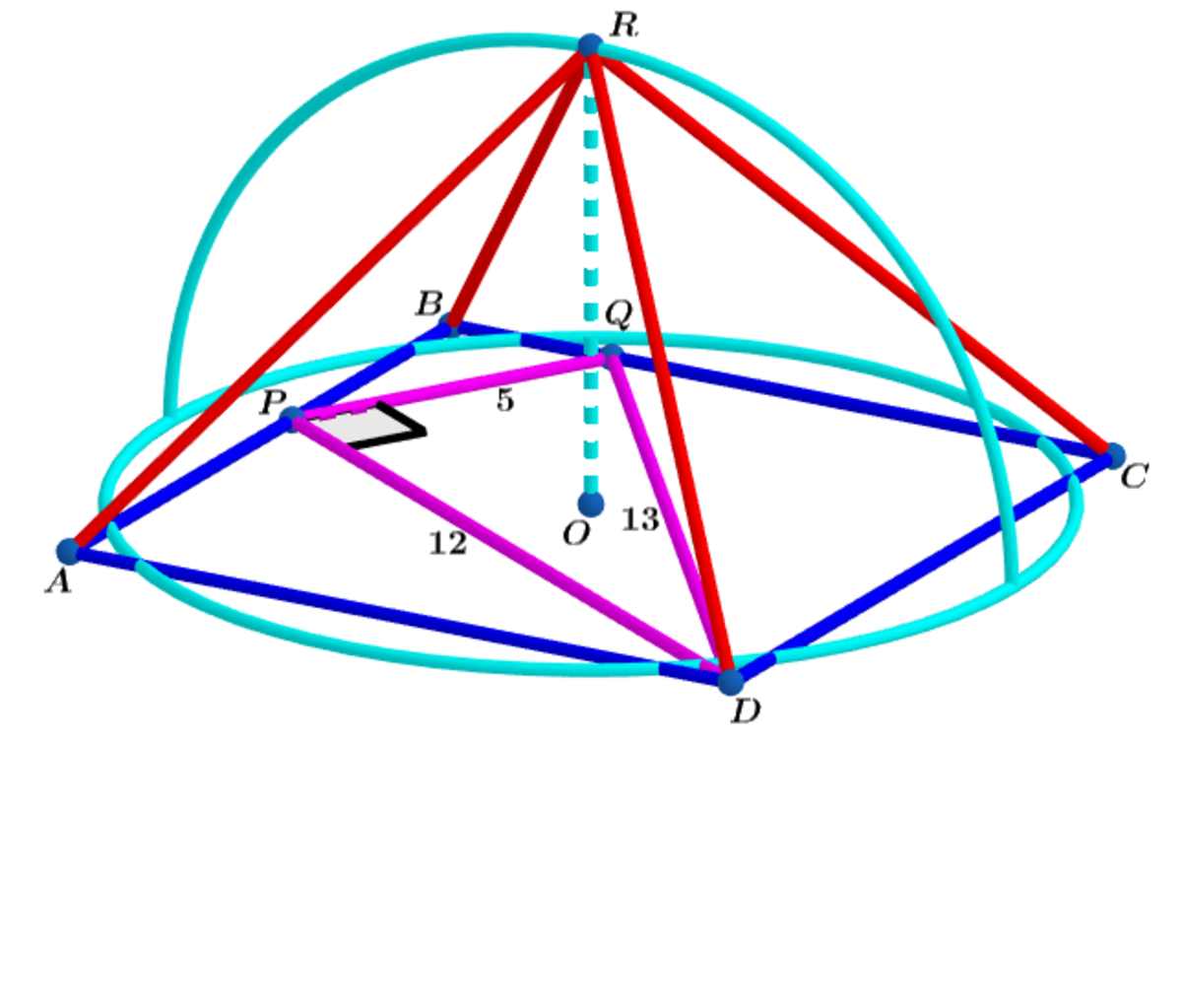
In square base , right forms the primitive pythagorean triple and is inscribed in square as shown above.
Let be the center of square and construct a circle centered at whose circumference is equal to the perimeter of the square. Folding the arc of the semi-circle at a right angle, as shown above, the radius of the semicircle becomes the height of the right square pyramid.
If the lateral surface area can be expressed as , where and are coprime positive integers, find .
The answer is 20945.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For the square base:
I generalized the problem using M and N as shown above. At the end of the problem I will replace the given values ( M = 5 , N = 1 2 ) .
Using the above diagram △ A P D ∼ △ P B Q ⟹ M N = x a ⟹ a = M N x ⟹
y = M N x − x = ( M N − M ) x ⟹ ( M 2 ( N − M ) 2 + M 2 N 2 ) x 2 = N 2 ⟹
x = ( N − M ) 2 + N 2 N M ⟹ a = ( N − M ) 2 + N 2 N 2
2 π r = 4 a ⟹ r = π 2 a ⟹ s = π 2 4 a 2 + 4 a 2 = 2 π a 1 6 + π 2 ⟹
The lateral surface area A = 4 ( 2 1 ) ( a ) ( 2 π a ) 1 6 + π 2 = π a 2 1 6 + π 2
= ( ( N − M ) 2 + N 2 ) π N 4 1 6 + π 2
Using M = 5 and N = 6 ⟹ A = 1 9 3 π 2 0 7 3 6 1 6 + π 2 = c ∗ π a b + π 2
⟹ a + b + c = 2 0 9 4 5 .