Right through the center
A solid sphere of radius R has a cylindrical hole drilled through it. The radius of the hole cylinder is 2 R , and its axis passes through the center of the sphere. This is depicted in the figure below. What percent of the sphere volume has been drilled out?
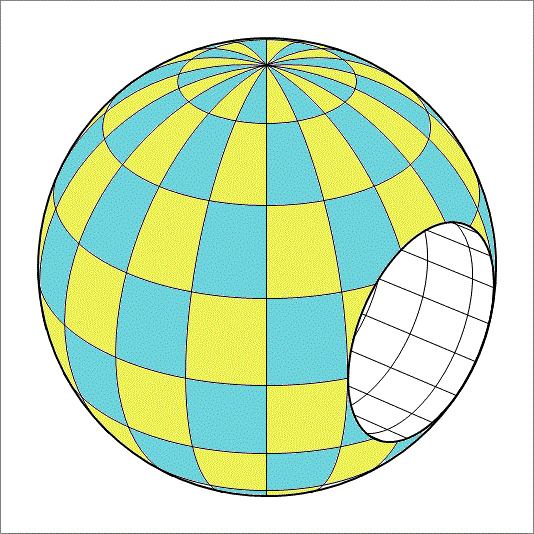
Note: This problem can be solved without resorting to numerical integration.
The answer is 35.05.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Did the same way.
A Spherical Ring is the solid of revolution of a cyclical segment
A
B
about a diameter
C
D
of its circle, which does not intersect the cyclical segment (figure 1).
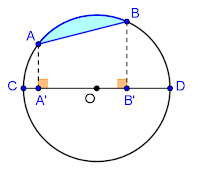 figure 1
The formula that calculates the volume of a spherical ring is
V
=
6
1
π
A
B
2
⋅
A
′
B
′
(
1
)
,
figure 1
The formula that calculates the volume of a spherical ring is
V
=
6
1
π
A
B
2
⋅
A
′
B
′
(
1
)
,
where
A
′
B
′
is the projection of cord
A
B
on the diameter of revolution.
In our case (figure 2),
A
A
′
=
2
R
=
2
O
A
, thus,
△
O
A
A
′
is a
1
-
3
-
2
triangle. Hence,
O
A
′
=
2
3
R
, therefore,
A
′
B
′
=
2
A
′
O
=
3
R
.
In addition,
A
B
is parallel to the axis of the hole, i.e.
A
B
∥
C
D
, thus,
A
B
=
A
′
B
′
=
3
R
.
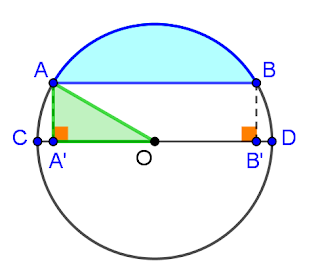 figure 1
figure 1
Using formula ( 1 ) , we have V r i n g = 6 1 π ( 3 R ) 3 = 2 3 π R 3 Finally, the percent of the sphere volume that has been drilled out is V s p h e r e V s p h e r e − V r i n g ⋅ 1 0 0 % = 3 4 π R 3 3 4 π R 3 − 2 3 π R 3 ⋅ 1 0 0 % = 8 8 − 3 3 ⋅ 1 0 0 % ≈ 3 5 . 0 5 %
W e u s e f o r m u l a ( 1 ) . I t i s c l e a r t h a t A B = A ′ B ′ ; A ′ O 2 = A O 2 − A A ′ 2 .
Log in to reply
There was a typo I edited. I think now it is correct and clear.
The hole is basically a cylinder with two spherical caps on each end. The following picture shows a cross-section of the sphere with the hole:
As given, the radius of the sphere is R = O A = O C = O D , and the radius of the cylinder is 2 1 R = A B = B C . By the Pythagorean Theorem on △ A B O , O B = 2 3 R , which means B D = O D − O B = R − 2 3 R = 2 2 − 3 R .
The volume of the cylinder is then V cyl = π r 2 h = π ⋅ ( 2 1 R ) 2 ⋅ 2 ⋅ 2 3 R = 4 3 π R 3 .
And the volume of one spherical cap is V cap = 3 1 π h 2 ( 3 R − h ) = 3 1 π ( 2 2 − 3 R ) 2 ( 3 R − ( 2 2 − 3 R ) ) = 2 4 1 6 − 9 3 π R 3 .
The percent of the sphere volume that has been drilled out is therefore p = V sphere V cyl + 2 V cap = 3 4 π R 3 4 3 π R 3 + 2 ( 2 4 1 6 − 9 3 π R 3 ) = 8 8 − 3 3 ≈ 3 5 . 0 5 % .