Right triangle
The figure shows a right triangle ABC at A , the perimeter of the triangle ABC = 60 cm , the length of AD = 12 cm. and AD is perpendicular to BC. Find the area of the triangle ABC , in
.
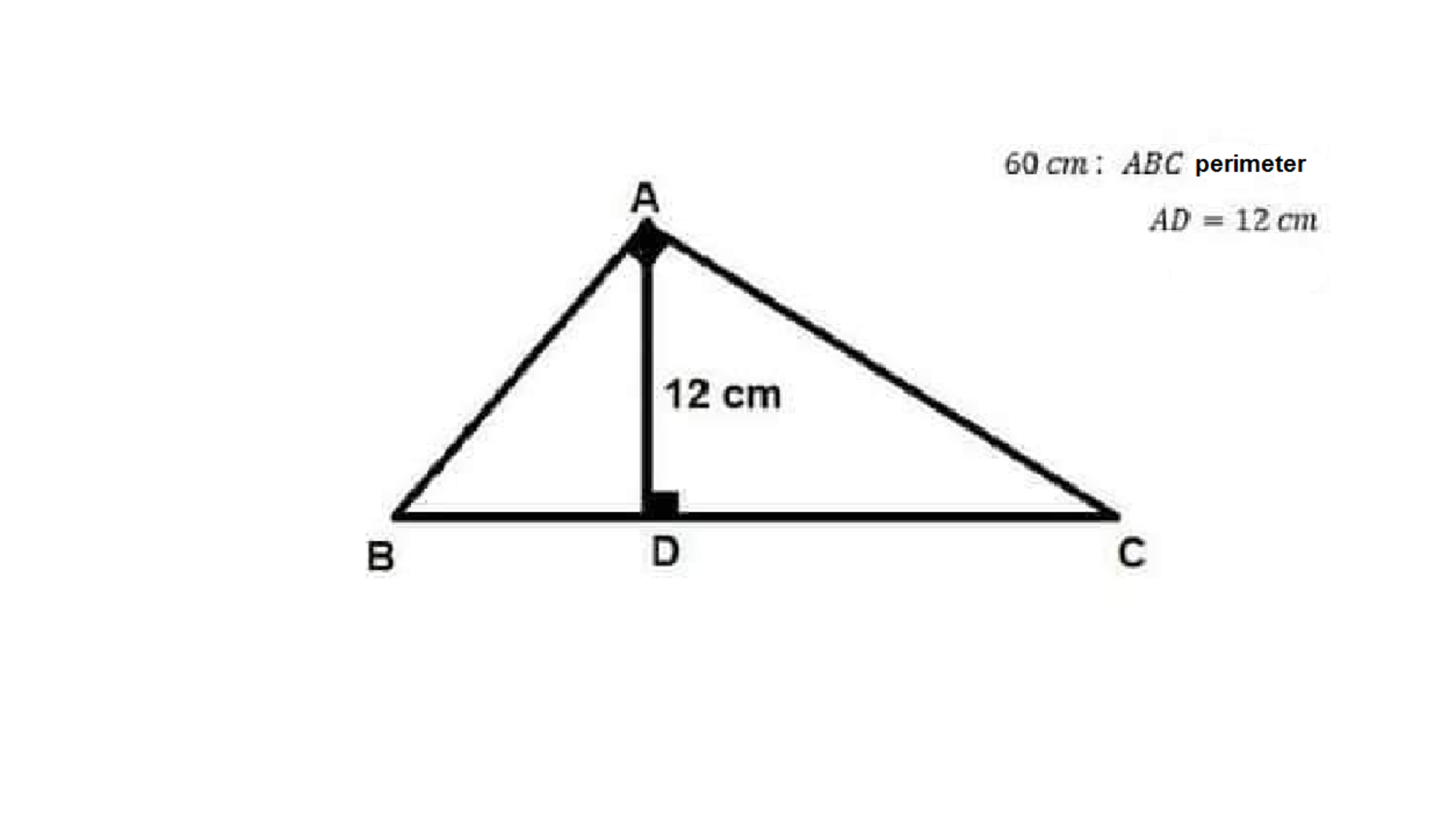
The answer is 150.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Quick Solution:
The ubiquitous 3 - 4 - 5 right triangle has a height of 2 . 4 if we treat the hypotenuse as the base (because b h = b h ⟹ 3 ⋅ 4 = 5 ⋅ h ).
We scale it by a factor of 5 , and try the new side lengths: 1 5 + 2 0 + 2 5 = 6 0 , so we have the "right" triangle, and its area is 2 1 ( 2 5 ) ( 1 2 ) = 1 5 0 cm 2
Slightly Longer Solution:
We label the sides of the given triangle in the traditional way (side a is opposite ∠ A etc.). We have the following system:
1 2 a a + b + c b 2 + c 2 = b c = 6 0 = a 2 ( 1 ) ( 2 ) ( 3 )
Rewriting ( 2 ) and squaring gives us
b + c b 2 + 2 b c + c 2 = 6 0 − a = 3 6 0 0 − 1 2 0 a + a 2
Now substituting in ( 1 ) and ( 3 ) , we get
a 2 + 2 4 a 1 4 4 a a = 3 6 0 0 − 1 2 0 a + a 2 = 3 6 0 0 = 2 5
Then, as above, the area is 2 1 ( 2 5 ) ( 1 2 ) = 1 5 0 cm 2