Right Triangle Inscribed in a Square

Geometry Level 3

In the diagram above, $\triangle{DEF}$ is a right triangle inscribed in square $ABCD$ . If $\overline{FE} = 3$ and $\overline{ED} = 4$ , then what is the area, to three decimal places without rounding, of square $ABCD$ ?

The answer is 15.058.

2 solutions

Chew-Seong Cheong
Jul 7, 2018

Relevant wiki: Pythagorean Theorem

Let the side length of square $ABCD$ be $a$ , $AE=x$ and $CF=y$ . Then by Pythagorean theorem we have:

$\begin{cases} a^2 + x^2 = 4^2 & ...(1) \\ a^2+y^2 = 5^2 & ...(2) \\ (a-x)^2+(a-y)^2 = 3^2 & ...(3) \end{cases}$

Solving the system of equation, we have $a \approx 3.88057$ and area of square $ABCD$ , $a^2 \approx \boxed{15.059}$ .

There are 2 solutions of positive triplets $(a,x,y)$ that satisfies all the 3 equations above, $(a,x,y) = \left(\dfrac{16}{\sqrt{17}}, \dfrac{4}{\sqrt{17}}, \dfrac{13}{\sqrt{17}} \right), \left(\dfrac{16}{\sqrt{65}}, \dfrac{28}{\sqrt{65}}, \dfrac{37}{\sqrt{65}} \right)$ .

You still need to add a condition that $x$ and $y$ are smaller than $a$ .

Pi Han Goh - 2 years, 11 months ago

A Former Brilliant Member
Jul 9, 2018

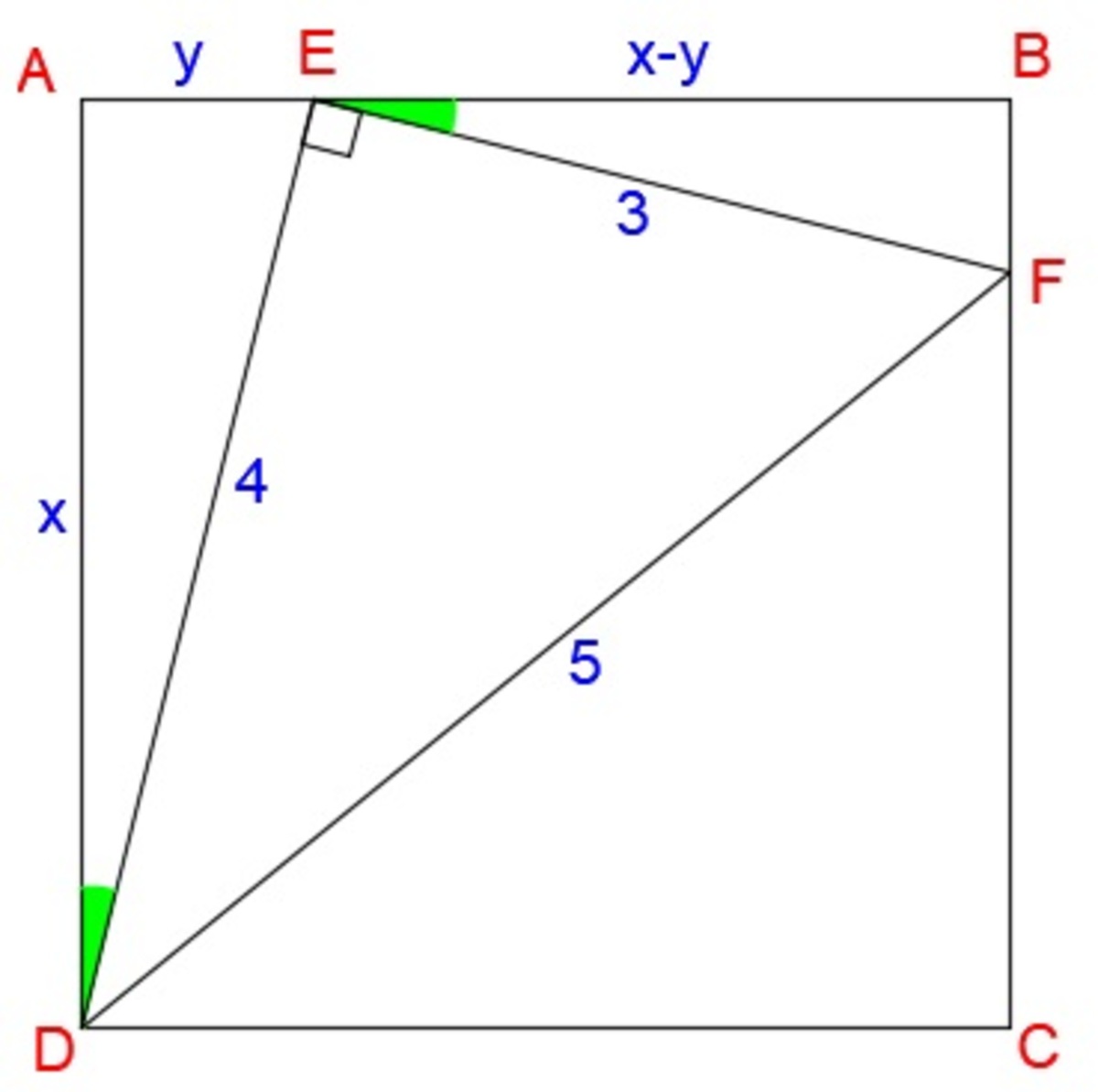Let $AD=x$ and $AE=y$ , then $EB=x-y$ . Since $\triangle ADE \sim \triangle BEF$ , we have

$\dfrac{x}{4}=\dfrac{x-y}{3}$

$3x=4x-4y$

$x=4y$

$y=\dfrac{x}{4}$

Apply pythagorean theorem on $\triangle DAE$ , we have

$x^2+y^2=4^2$

$x^2+y^2=16$

Substitute $y=\dfrac{x}{4}$ to the above equation, we have

$x^2 + \left(\dfrac{x}{4}\right)^2=16$

$x^2+ \dfrac{x^2}{16}=16$

$\dfrac{17}{16}x^2=16$

$x^2=\dfrac{256}{17} \approx 15.05882353$

Right Triangle Inscribed in a Square

The answer is 15.058.

2 solutions

0 pending reports