Right triangle, perimeter = area?
Find all the right triangles with integer side lengths such that their perimeter and area have the same numerical value.
Submit your answer as the sum of all possible numerical values mentioned above.
The answer is 54.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Euclid's formula is a way to generate infinitely many Pythagorean triples, but it doesn't give us an exhaustive list. It's insufficiently general, according to the wiki.
The hypotenuse wasn't also supposed to be a integer? In this case, there wouldn't be any solution.
Log in to reply
Correct, if we required that the hypotenuse not be an integer then there would be no solutions. But this isn't what the problem stipulates.
If a , b , and a 2 + b 2 are the sides of a right triangle, then P = a + b + a 2 + b 2 and A = 2 a b . Equating both expressions yields
a 2 + b 2 = 4 a 2 b 2 − a b 2 − a 2 b + 2 a b + a 2 + b 2
which simplifies to
a + b = 4 a b + 2 ( 1 )
Since a , b ∈ N , it follows that 4 a b ∈ N , and 4 divides a or b , or 2 divides both a and b . In the latter case, letting a = 2 p and b = 2 q , we find that 2 p + 2 q = p q + 2 . Therefore, 2 divides p or q , and so either a or b is divisible by 4 , which was the former case.
Suppose that b = 4 m for some positive integer m . Substituting ( 1 ) , we get a + 4 m = a m + 2 . Since this can be written as
( a − 4 ) + 2 = ( a − 4 ) m
we see that ( a − 4 ) ∣ 2 . Thus, the only solutions to our problem occur for a = 5 and a = 6 , with respective values b = 1 2 and b = 8 . Their corresponding areas are
A A = 2 1 ⋅ 5 ⋅ 1 2 = 3 0 = 2 1 ⋅ 6 ⋅ 8 = 2 4
Our answer is 5 4 .
Nice work. Once you get to your equation (1), it might also be convenient to write it as a b − 4 a − 4 b + 8 = 0 , so you can see how it factors: ( a − 4 ) ( b − 4 ) = 8 . Then both the ways to split 8 into two factors, that is, ( 1 ) ( 8 ) and ( 2 ) ( 4 ) , generate the above solutions for a and b.
Log in to reply
Amazing insight! Thank you Seth :) That definitely would have cut down the work into easier, algebraic methods.
Wow I like your solution! Can anyone explain me what the | symbol means, smaller than or equal to???
Log in to reply
Thanks!
a ∣ b means that a divides b for integers a and b . In other words, there exists some integer k such that k ⋅ a = b .
Yes, this method is also known as Simon's favorite factoring trick .
Suppose the 3 sides of the right angled triangle is a , b and c , where a ≤ b ≤ c . Then
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ a + b + c = p 2 1 a b = p a 2 + b 2 = c 2 .
The first equation gives a + b = p − c , square both sides of the equation to obtain a 2 + b 2 + 2 a b = p 2 − 2 p c + c 2 .
The above equation can be simplified using the second and third equations: 4 p = p 2 − 2 p c .
This implies that c = 2 p − 4 . Thus a + b = p − 2 p − 4 = 2 p + 4 .
From a + b = 2 p + 4 and a b = 2 p , we know that a and b are roots of x 2 − 2 ( p + 4 ) x + 2 p = 0 .
Since a and b are integers, the discriminant is a perfect square, i.e. ( 2 p + 4 ) 2 − 4 ( 1 ) ( 2 p ) = k 2 , where k > 0 is an integer. This equation is equivalent to p 2 − 2 4 p + 1 6 = ( 2 k ) 2 , which can be written as ( p − 1 2 + 2 k ) ( p − 1 2 − 2 k ) = 1 2 8 = 2 7 . As p − 1 2 + 2 k and p − 1 2 − 2 k has the same parity, and p − 1 2 + 2 k > p − 1 2 − 2 k , we have the following possibles cases.
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ p − 1 2 + 2 k = 6 4 and p − 1 2 − 2 k = 2 p − 1 2 + 2 k = 3 2 and p − 1 2 − 2 k = 4 p − 1 2 + 2 k = 1 6 and p − 1 2 − 2 k = 8 .
The first case give non-integer k , and it is rejected. Solving for the second and the third cases give p = 3 0 and p = 2 4 respectively.
Hence the sum of all such p is 5 4 .
Check: if p = 3 0 , ( a , b , c ) = ( 5 , 1 2 , 1 3 ) ; if p = 2 4 , ( a , b , c ) = ( 6 , 8 , 1 0 ) .
The question is unclear. Knowing the two triangles were (5,12,13) and (6,8,10), I could not decide what "all possible numerical values mentioned above" meant.
Assume the legs are x and y . W.l.o.g, x ≥ y .
Perimeter = x + y + x 2 + y 2
Area = 2 x y
∴ x + y + x 2 + y 2 = 2 x y
After squaring and rearranging the equation,
x y − 4 x − 4 y + 8 = 0
( x − 4 ) ( y − 4 ) = 8 = 8 × 1 = 4 × 2
So the solutions are ( x , y ) = ( 1 2 , 5 ) , ( 6 , 8 )
Both solutions are accepted since x 2 + y 2 are positive integers. Namely 13 and 10 respectively.
W = 2 x y = 3 0 or 2 4
∴ ∑ W = 5 4
Euclid's formula for Pythagorean Triples states that the sides of a right angled triangle must be in the form of m 2 − n 2 , 2 m n and m 2 + n 2 , where m , n are both postive integers.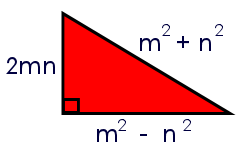 Hence we can now equate the area and perimeter:
Hence we can now equate the area and perimeter:
2 1 ( 2 m n ) ( m 2 − n 2 ) = ( m 2 + n 2 ) + ( m 2 − n 2 ) + ( 2 m n )
m n ( m 2 − n 2 ) = 2 m 2 + 2 m n
m n ( m + n ) ( m − n ) = 2 m ( m + n )
m n ( m − n ) = 2 m
n ( m − n ) = 2
From this we obtain the 2 solutions for ( m , n ) which are ( 3 , 1 ) and ( 3 , 2 ) since 2 only has 2 factors. Substituting these values back into the side lengths of the triangle, we obtain the 6 − 8 − 1 0 triangle with area and perimeter of 2 4 and the 5 − 1 2 − 1 3 triangle with area and perimeter 3 0 .
Hence 2 4 + 3 0 = 5 4