Right Triangle Propogation
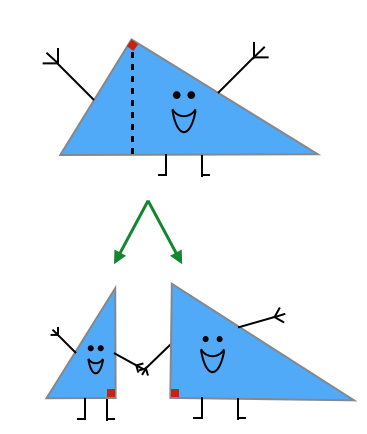If you use a single, straight cut to make one right triangle into two, smaller right triangles; what can you say about the two offspring triangles in comparison to their parent?
I. Neither offspring can be
congruent
to the parent.
II. Both offspring are definitely
congruent
to the parent
III. Neither offspring can be
similar
to the parent.
IV. One or both offspring might be
similar
to the parent, or not.
V. Both offspring are definitely
similar
to the parent.
Dissimilar Right Triangle Party!!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I and II: Neither of the smaller triangles can be congruent to their parent because both of them only share one congruent angle and one congruent side with their parent, which is not enough to prove that the triangles are congruent. Therefore, I is true.
III, IV, and V: Both of the smaller triangles share two congruent angles with the parent triangle: the right angle made by cutting the parent triangle, and the angle directly across from the smaller triangles' heights (which is the same angle as the one in the parent triangle). By AA similarity, we can prove that the each of the smaller triangles are similar to their parent. Therefore, V is true.