Right Triangles Galore
From the figure below, A B C and D E F are right triangles, and A F and D C are the their respective altitudes. Point G is the intersection of A C and D F and G H is drawn from it such that it is perpendicular to B C . If A F = 6 and G H = 4 and F C = 9 , what is the area of polygon A G D E B ?
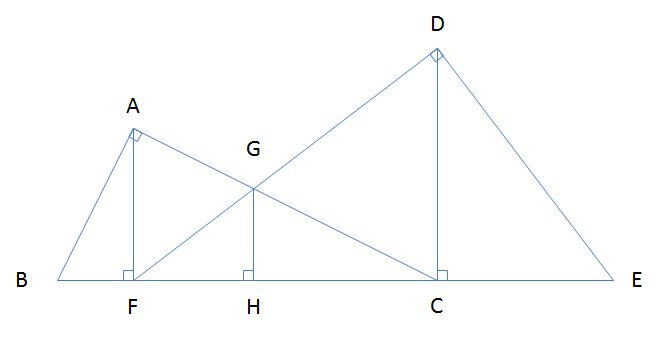
The answer is 171.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Can you explain for the first equation? How do you have that to solve DC?
Since △ AFC and △ GHC are similar, we get CH = 3 2 ∗ 9 = 6 and FH =3
Since △ DCF and △ EDF are similar, D F E D = C F D C = 9 1 2
Since △ DCE and △ FDE are similar, E D D F = C E D C = 1 2 9 from above
So we get, CE = 16. Similarly, we can get BF = 4.
(The above can also be obtained by using, D C 2 = C E . C F and A F 2 = B F . C F )
Area of polygon AGDEB
= Area △ ABC + Area △ DEF - Area △ GFC
= 39 + 150 - 18 = 171
How is AFC and GFC similar? Your proof for that?
Log in to reply
sorry...I meant AFC and GHC..I have made the correction.. Thank you!
Relevant wiki: Similar Triangles - Problem Solving - Medium
From similar triangles, A F 1 + D C 1 = G H 1 . Solving for D C , we get D C = 1 2 .
For right triangles, ( B F ) ( F C ) = A F and ( F C ) ( C E ) = D C . Solving for B F and C E we get B F = 4 and C E = 1 6 .
Area of polygon A G D E B is equal to [ A B C ] + [ D E F ] − [ G F C ] = 2 1 3 × 6 + 2 2 5 × 1 2 − 2 4 × 9 = 1 7 1 .