Right Trig of Eq Perimeter
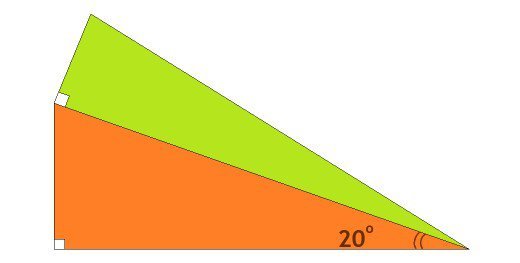
The two right triangles shown below have equal perimeters. The hypotenuse of the orange triangle is one leg of the green triangle stacked on top of it. If the smallest angle of the orange triangles is 20 degrees, what is one of the angles of the green right triangle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We don't need to know the side length of the triangles to solve for the unknown angles, only their relative lengths are necessary, let the two legs of the orange triangle be cos(20) and sin(20), and let the hypotenuse equal 1. The green triangle then has one leg of length 1, another length of unknown length X, and a hypotenuse of sqrt(X^2 + 1). Since the two triangles' perimeters are equal, we have the equation
sin(20) + cos(20) + 1 = 1 + X + sqrt(X^2 + 1)
sin(20) + cos(20) = X + sqrt(X^2 + 1)
If we use the technique for solving algebraic equations with square root and linear terms, we get
[sin(20) + cos(20) - X]^2 = X^2 + 1
sin(20)^2 + 2sin(20)cos(20) + 2cos(20)^2 - 2sin(20)X - cos(20)X + X^2 = X^2 + 1
1 + 2sin(20)cos(20) - 2sin(20)X - 2cos(20)X + X^2 = X^2 + 1
2sin(20)cos(20) - 2sin(20)X - 2cos(20)X = 0
X = sin(20)cos(20)/[sin(20 + cos(20)] ≈ 0.250753
The angles of the green triangle are 90 degrees, arctan(X/1) ≈ 14.08 degrees, and arctan(1/X) ≈ 75.92 degrees.