Right Triangle's Variable Sides
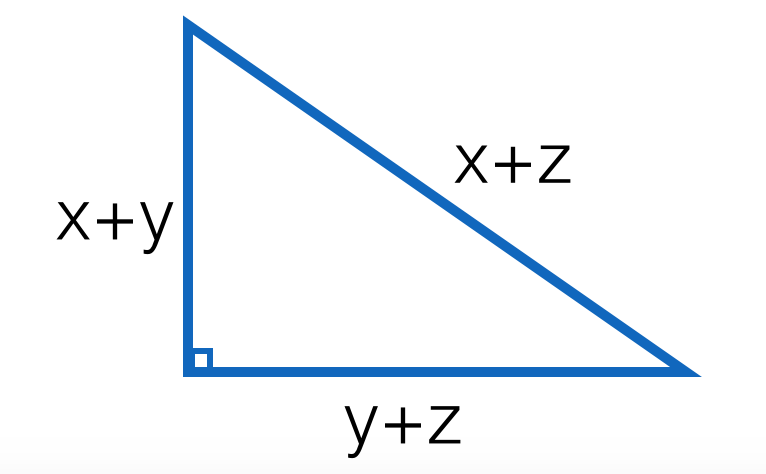 In a certain right triangle, the hypotenuse equals
(
x
+
z
)
while the other two sides are
(
x
+
y
)
and
(
y
+
z
)
for positive integers
x
,
y
,
z
.
In a certain right triangle, the hypotenuse equals
(
x
+
z
)
while the other two sides are
(
x
+
y
)
and
(
y
+
z
)
for positive integers
x
,
y
,
z
.
If y + 4 = z and z > x , then compute x z .
The answer is 1.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
I was too close
I don't get it?
Is it possible split z 2 − 6 z − ( 2 x − 8 ) = 0 as z 2 − 6 z = 0 and 2 x − 8 = 0 so you obtain soon x = 4 and z = 6 ?
Since x+z is only 4 greater than x+y, we can find any right triangle that satisfies that one of the leg is 4 less than the hypotenuse. Note that y+z needs to have length between the other two, so the right triangle has small integer length. 6-8-10 comes up as a matching triangle. 8 is between the other two, which means y+z=8. y+z=8 =>y+y+4=8 =>y=2 =>x=4 =>z=6 Hence 6/4 = 1.5.
Or do it the stupid long algebra way. That's also correct.
Could you elaborate more on your explanation ? how many trials did you come up in order to reach your solution of 6-8-10 ? I want to measure the time spent doing this against the algebra path. It doesn't seem to be fast to reach the 6-8-10 triangle. Regards
Log in to reply
There are known, common, integer-sided right triangles. The most basic one, I think is a 3-4-5. (where 9 + 16 = 25). So integer multiples of 3-4-5 will also be right triangles ( I think). 6-8-10 is twice the sizes of a 3-4-5. So Glenn tried that one first because there is one leg that's the size of another + 4. And it worked.
Yeah hahaha :D
We have
y
+
4
=
z
, which is the same as
(
x
+
y
)
+
4
=
(
x
+
z
)
. Therefore, the hypotenuse is
4
more than one of the sides of the right angled triangle. Let
x
+
z
=
h
+
2
and
x
+
y
=
h
−
2
, for some
h
>
2
. Then by the Pythagoras' Theorem,
(
y
+
z
)
2
=
(
h
+
2
)
2
−
(
h
−
2
)
2
=
8
h
, so
8
h
must be a perfect square(and it is even). Let
8
h
=
4
k
2
, for some natural number
k
. Then
y
+
z
=
2
k
, and
x
+
y
=
2
k
2
−
2
so
k
is even and is greater than
2
. Finally,
z
>
x
implies
y
+
z
>
y
+
x
, or
2
k
>
2
k
2
−
2
, or
k
2
−
4
k
<
8
.
This means
(
k
−
2
)
2
<
1
2
.
Recall that
k
must be even, so
k
=
2
,
4
. But
k
>
2
. Therefore
k
=
4
. So the sides of the triangle are
2
×
4
=
8
,
2
4
2
−
2
=
6
,
and 10.
Note that
2
x
+
2
y
+
2
z
=
6
+
8
+
1
0
=
2
4
, so
x
+
y
+
z
=
1
2
Therefore
z
=
1
2
−
(
x
+
y
)
=
6
,
and
x
=
1
2
−
(
y
+
z
)
=
4
. So
x
z
=
1
.
5
Nice method
Your solution is elegant enough :)
y= 1 + 2 x − 1
and z= 1 + 2 x + 3
x,y,z all are positive integers and ,
from triangle inequality we can say z > x > y > 0 ,
z is also 4 more than 'y'
now,x=4 gives y=2 , z=6 therefore,
x z = 1 . 5

z=3 doesn't satisfy y+4=z but we have positive integers where they obey the above conditions
notice that i didn't work for the real triangle values for x,y,z
By Pythagoras, we have that
(x+z)^2 = (x+y)^2 + (y+z)^2
Substituting for y=z-4
(x+z)^2 = (x+z-4)^2 + (2z-4)^2
Expand, rearrange and factor yields
0 = (z-4)(z-2) - 2x
As x>0 ,(z-4)(z-2) must be >0 which implies that z<2 or z>4
Given that z>0, this implies that z=1 or z>4
As z>x, z=1 would imply that x (also a positive integer) would be 0, hence z cannot be = 1
Trialling z=5 (first integer greater than 4) yields a non-integer value for x
Trialling z=6 yields x=4 which satisfies all conditions and 6/4 = 1.5
x + y + y + z ≥ x + z
z ≥ 4
( x + y ) 2 + ( y + z ) 2 = ( y + z )
After much simplification
2 y 2 + 4 y − 4 x = 0
Discriminant = 4 2 − 4 ⋅ 2 ⋅ 4 x = 1 6 + 3 2 x
Discriminant needs to be a perfect square as x , y , z integers.
With some trial and error you get x = 4
And after that y = 2 and z = 6 and x = 4 .
So, x z = 4 6 = 1 . 5
By replacing y=z-4 and then using Pythagoras theorem We get z^2 - 6z +8 -2x=0 Now doing a bit of factorization we get (z-4) (z-2)=2*x
Now doing some logical comparison of both side we get z=6 ;x=4 So z÷x=1.5
What is that logical reasoning?

By Pythagoras, we have that
( x + z ) 2 = ( x + y ) 2 + ( y + z ) 2
⟹ x 2 + 2 x z + z 2 = ( x 2 + 2 x y + y 2 ) + ( y 2 + 2 y z + z 2 )
⟹ 2 x z = 2 x y + 2 y z + 2 y 2 = 2 y ( x + y + z ) ⟹ x z = y ( x + y + z ) .
Given that y = z − 4 , this last equation then becomes
x z = ( z − 4 ) ( x + 2 z − 4 ) ⟹ x z = x z + 2 z 2 − 4 z − 4 x − 8 z + 1 6
⟹ z 2 − 6 z − ( 2 x − 8 ) = 0
⟹ z = 2 6 ± 3 6 + 4 ( 2 x − 8 ) = 3 ± 1 + 2 x .
Now since x and z must be positive integers, we will require that 1 + 2 x be a perfect square, and since 1 + 2 x is odd this perfect square must be that of an odd number. (Also, as this odd perfect square will be ≥ 3 we just need to look at the positive root, (since z > 0 ).) Thus for integers k > 0 we require that
1 + 2 x = ( 2 k + 1 ) 2 ⟹ 1 + 2 x = 4 k 2 + 4 k + 1 ⟹ x = 2 k ( k + 1 ) .
For k = 1 we have ( x , z ) = ( 4 , 6 ) , and for k = 2 we have ( x , z ) = ( 1 2 , 8 ) . In fact for k ≥ 2 we will have z < x , so since we must also satisfy the condition z > x we are left with the unique solution ( x , y , z ) = ( 4 , 2 , 6 ) , which yields a 6 / 8 / 1 0 right triangle and the ratio x z = 4 6 = 1 . 5 .