Right within Equilateral

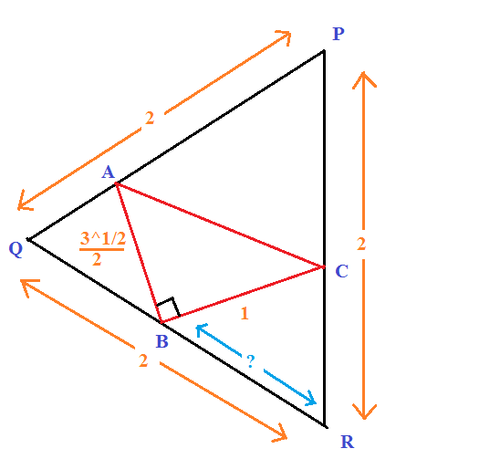
Since nobody is posting a solution (only 2 solvers till now though) and there are many who could not solve it, i think id better post one. So here it goes. First let $\angle QBA = x$ . Then $\angle CBR = 90^{\circ} - x$ . Note $\angle Q = \angle R = \angle P = 60^{\circ}$

Applying Law's of sines in $\triangle QBA$ , we have

$\dfrac{QB}{\sin(120^{\circ} -x)} =\dfrac{AB}{\sin60^{\circ}}= \dfrac{\frac{\sqrt{3}}{2}}{sin60^{\circ}} = 1$

$\implies BQ = \sin(120^{\circ} -x) ...... (i)$

Again applying Laws of sines in $\triangle RBC$ we will have after some simplification

$BR = \dfrac{2\sin(30^{\circ} + x)}{\sqrt{3}}..... (ii)$

Adding $(i)$ and $(ii)$ we get

$BQ + BR = \sin(120^{\circ} -x) + \dfrac{2\sin(30^{\circ} + x)}{\sqrt{3}}$

$\implies 2 = \sin(120^{\circ} -x) + \dfrac{2\sin(30^{\circ} + x)}{\sqrt{3}}$

$\implies 2\sqrt{3} = \sqrt{3} \sin(120^{\circ} -x) + 2\sin(30^{\circ} + x)$

After breaking up the compound angles by the well known formula and furthur simplifations we have

$4\sqrt{3} = 5\cos x + 3\sqrt{3}\sin x$ $\implies \sqrt{3}(4 - 3\sin x) = 5 \cos x$

Now squaring both sides and using $\cos^2 x + sin^2 x = 1$ we have

$52\sin^2 x - 72\sin x + 23 = 0$ $\implies (2\sin x - 1)(26\sin x - 23) = 0$

Therefore either $\sin x = \frac{1}{2} \implies x = 30^{\circ}$ or $\sin x = \frac{23}{26}$

$x = 30^{\circ}$ implies $\triangle CRB$ is equilateral and hence $\large{\boxed{BR =1}}$ . And if $\sin x = \frac{23}{26}$ , $\cos x = \dfrac{7\sqrt{3}}{26}$ . Therefore we have

$BR = \dfrac{2}{\sqrt{3}} ( \dfrac{\cos x}{2} + \dfrac{\sqrt{3}\sin x}{2})$

$= \dfrac{2}{\sqrt{3}} ( \dfrac{7\sqrt{3}}{2 \times 26} + \dfrac{\sqrt{3} \times 23}{2 \times 20}$

$= \dfrac{7}{26} + \dfrac{23}{26} = \dfrac{30}{26}$ $\implies \large{\boxed{ BR = \dfrac{15}{13}}}$

Hence the sum of all possible values of $BR$ is $1 + \dfrac{15}{13} = \dfrac{13 + 15}{13} = \dfrac{28}{13}$

Hence $a+b = 28 + 13 = \large{\boxed{41}}$