The Eternal Ring!
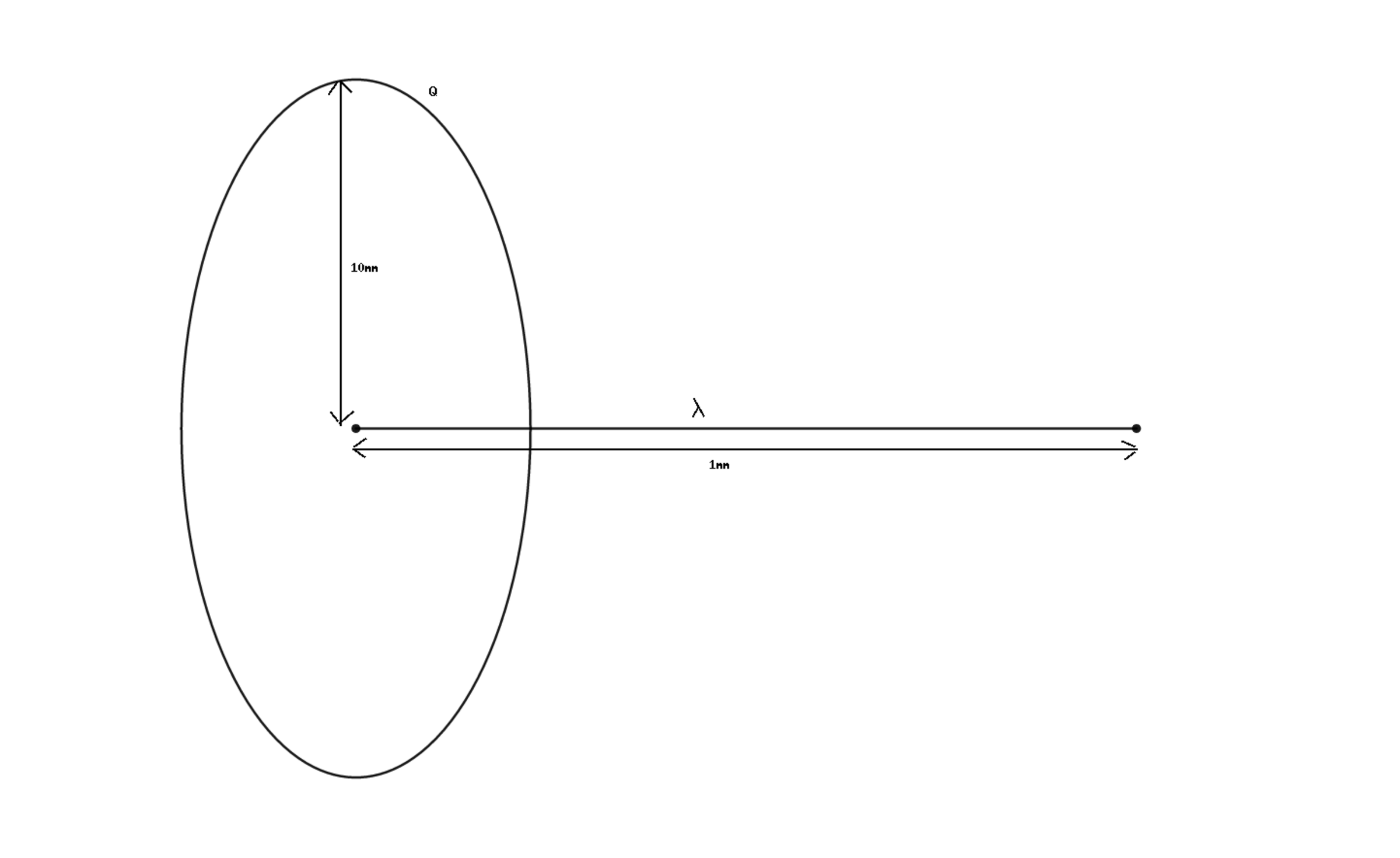
A fixed line charge of linear charge density λ = + 0 . 1 μ C/m and length L = 1 mm is placed coaxially to a free ring of charge Q = − 1 μ C , radius R = 1 0 mm and mass m = 9 0 0 g . The ring is released from rest from one end of rod. Find time period of ring(in sec).
Ignore gravity and air resistance. Take 4 π ϵ o 1 = 9 × 1 0 9 Nm 2 / C 2 .
All of my problems are original .
The answer is 6.283.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Fun problem. I modeled this using numerical integration over time. On every time step, the program integrates over the length of the rod to get the total force. Due to symmetry, the ring can be modeled as an equivalent point charge a distance R from the rod axis, and we consider only the force parallel to the rod axis. My highest resolution simulation uses a time step of 1 0 − 4 seconds and a spatial step (on the rod) of 1 0 − 7 meters. The convergence is quite good, and the time period comes out to T ≈ 6 . 3 0 4 . Note that this simulation does not require or use series expansions.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 |
|
Excellent solution sir. Thanku for sharing. :)
My first instinct was to perform a time domain simulation. But since the parameters have such small orders of magnitude, I thought that the resulting system of ODEs might be numerically not easy to handle (numerical stiffness). I thought that smaller time steps would be necessary. But it is surprising to see that time steps in the order of milliseconds works well.
Log in to reply
I looked at the force, and realized it would be about 1 0 − 2 N . Acting on a 1 k g mass, the motion should be nice and slow (relative to a time step of 1 0 − 3 or 1 0 − 4 seconds)
Log in to reply
Yes, I just tried the numerical route and now I see this for myself. I would have solved it faster if I made this observation early. Good one!
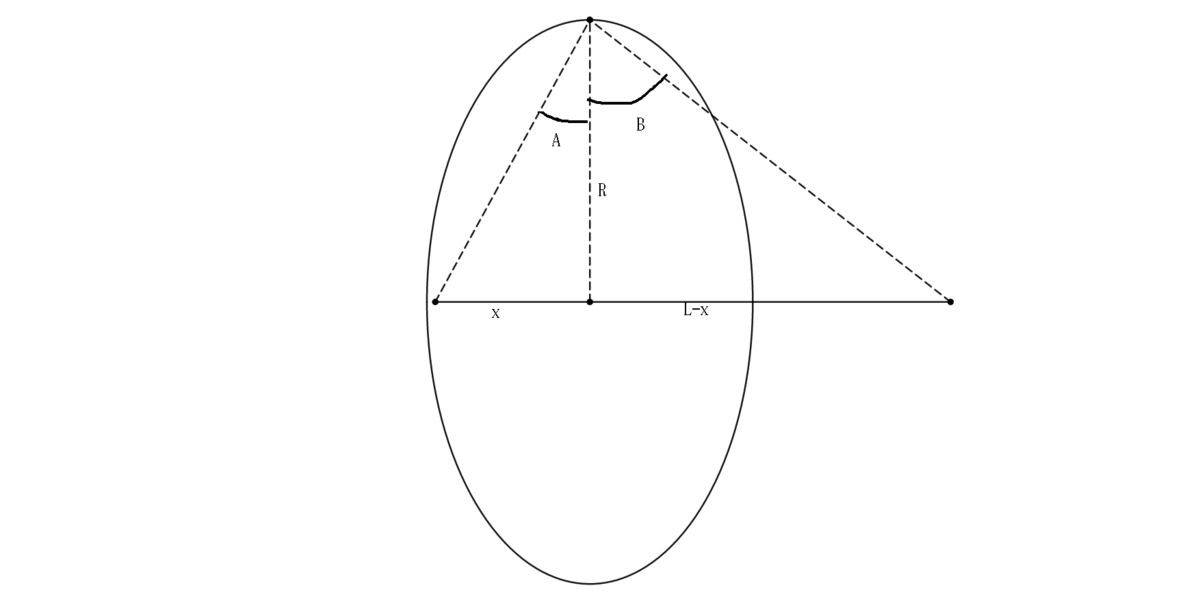
Force on ring by rod can be given by F = 4 π ϵ o 1 R λ Q ( R 2 + x 2 R − R 2 + ( L − x ) 2 R ) F = 4 π ϵ o 1 R λ Q ( 1 + ( R x ) 2 1 − 1 + ( R L − x ) 2 1 )
As maximum value of ( R x ) 2 = 0 . 0 1 , in binomial expansion of ( 1 − R x ) − 2 1 , we can ignore powers of x greater than 2. Same is true for ( R L − x ) term.
F = 4 π ϵ o 1 R λ Q ( ( 1 − 2 1 ( R x ) 2 ) − ( 1 − 2 1 ( R L − x ) 2 ) ) F = 4 π ϵ o 1 R 3 λ Q L ( 2 L − x )
So, above motion represents SHM about x = L / 2 . Force constant can be given by
k = 4 π ϵ o 1 R 3 λ Q L
k = 0 . 9
So, time period T can be given as
T = 2 π k m
T = 2 π sec
T = 6 . 2 8 3 sec
Mine is a different approach from that of @Steven Chase
Consider the left end of the wire to be the origin. Say the ring has moved a distance x from the left end. At this instant, the potential energy of the system can be computed as such:
V = − ∫ 0 L R 2 + ( p − x ) 2 K Q λ d p
This integral transforms to:
V = − K Q λ ∫ − x L − x R 2 + z 2 d z = − K Q λ ( sinh − 1 ( R L − x ) − sinh − 1 ( R − x ) )
At the instant when the ring is released from rest, the potential energy is:
V o = − K Q λ ∫ 0 L R 2 + z 2 d z = − K Q λ sinh − 1 ( R L )
At a general time t , applying the law of conservation of energy leads to:
2 M x ˙ 2 + V = V o ⟹ 2 M x ˙ 2 = K Q λ ( sinh − 1 ( R L − x ) − sinh − 1 ( R − x ) − sinh − 1 ( R L ) ) ⟹ x ˙ = M 2 K Q λ ( sinh − 1 ( R L − x ) − sinh − 1 ( R − x ) − sinh − 1 ( R L ) )
Separating the variables and integrating from 0 to L gives half the time period.
⟹ T = 2 ∫ 0 L M 2 K Q λ ( sinh − 1 ( R L − x ) − sinh − 1 ( R − x ) − sinh − 1 ( R L ) ) d x ≈ 6 . 3
This last step was solved numerically.