Ring-Race
 This question would amplify your skills in Kinematics.
This question would amplify your skills in Kinematics.
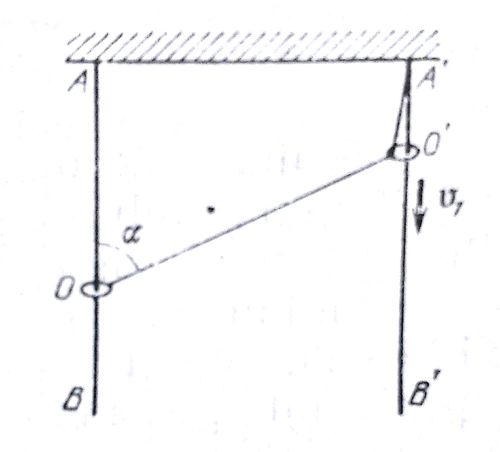
Two rings O and O' are put two vertical stationary rods AB and A'B'. An inextensible thread is fixed at point A' and on the ring O and is passed through the ring O'. Assuming O' moves downwards constantly with , determine velocity if └AOO' is α. If the answer can be expressed as a ( ))/cosα. Find a+b+c
Also try : Optics or ClassicalMechanics
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Sorry for not marking α = ∠ DEC = ∠ CAB
Since they are rods( inelastic) , this would be the condition (thread becomes horizontal)
A to ceiling =' l ' , AB = a , BC = b , AC = c , CD = d , DE = e , CE = f
a 2 + b 2 = c 2
Diffrentiating with respect to time .
d t d c = vcos α ( as b = const . )
Similarly , d 2 + e 2 = f 2
d t d e = sec α d t d f
Since length of rope is constant -
l + c+ f = l + a + b + d
c+f = a + b + d
Diff . with respect to time -
d t d f = v( 1 - cos α )
d t d e = sec α d t d f = sec α v( 1 - cos α )
d t d e = Ans = 2 v sin^2 α / 2 / cos α