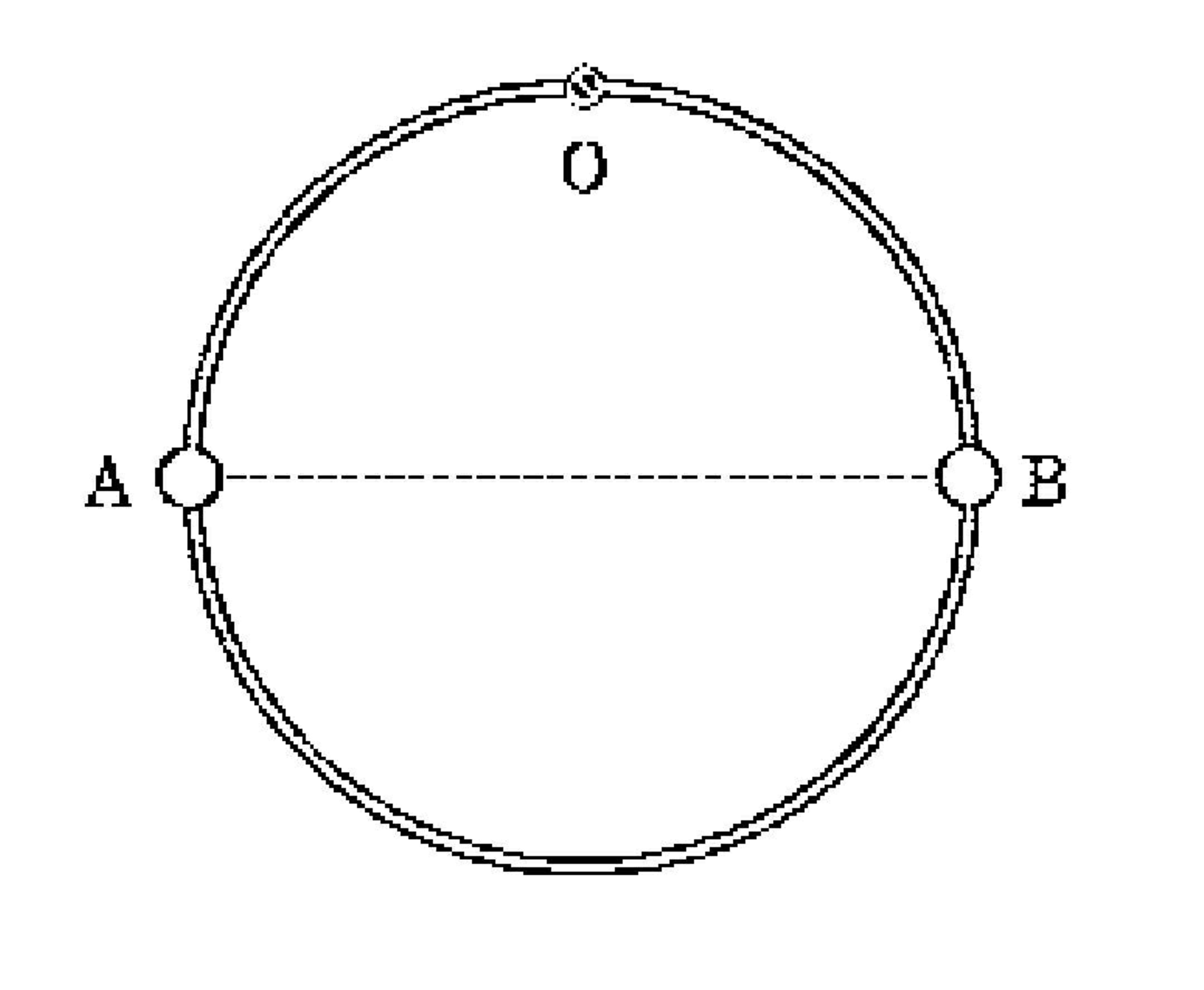
Ring with beads

I have used the Lagrangian formulation to solve this. Any other fundamental approach would be too tedious, in my opinion.

Say at a general time $t$ the ring has rotated anticlockwise about $O$ by $\theta$ . At the same time, B has rotated along the ring clockwise by an angle $\phi$ . Based on this, the coordinates of points A and B are:

$x_A = R\sin{\theta} - R \cos{\theta}$ $y_A = -R\cos{\theta} - R \sin{\theta}$

$x_B = R\sin{\theta} + R \cos(\phi-\theta)$ $y_B = -R\cos{\theta} - R \sin(\phi-\theta)$

I request the reader to try visualising the geometry and deriving the above coordinates by him/her self.

Having done the above, the kinetic energy of the system can be derived as such:

$\mathcal{T} = \frac{m}{2}(\dot{x}_A^2 + \dot{y}_A^2) + \frac{m}{2}(\dot{x}_B^2 + \dot{y}_B^2)$

The potential energy of the system is:

$\mathcal{V} = mgy_A + mgy_B$

After simplification, the expression turn out to be:

$\mathcal{T} = \frac{m}{2}\left(4R^2 \dot{\theta}^2 +R^2 \dot{\phi}^2 -2R^2\dot{\phi}\dot{\theta} +2R^2\dot{\theta} ^2\sin{\phi} - 2R^2\dot{\phi}\dot{\theta}\sin{\phi}\right)$

$\mathcal{V} = -mg(2R\cos{\theta} + R\sin{\theta} + R\sin(\phi-\theta ))$

Lagrange's equations read:

$\frac{d}{dt}\left(\frac{\partial \mathcal{T}}{\partial \dot{\theta}}\right) - \frac{\partial \mathcal{T}}{\partial \theta} + \frac{\partial \mathcal{V}}{\partial \theta}=0$

$\frac{d}{dt}\left(\frac{\partial \mathcal{T}}{\partial \dot{\phi}}\right) - \frac{\partial \mathcal{T}}{\partial \phi} + \frac{\partial \mathcal{V}}{\partial \phi}=0$

Doing this entire derivative crunching gives the required equations of motion which are:

$4mR^2 \ddot{\theta} - mR^2 \ddot{\phi} + 2mR^2\ddot{\theta}\sin{\phi} + 2mR^2\dot{\theta}\dot{\phi}\cos{\phi}- mR^2\ddot{\phi}\sin{\phi} - mR^2\dot{\phi}^2\cos{\phi} + 2mgR\sin{\theta} -mgR\cos{\theta} + mgR\cos(\phi - \theta)=0$

$mR^2 \ddot{\phi} - mR^2\ddot{\theta} - mR^2\ddot{\theta}\sin{\phi} - mR^2\dot{\theta}^2\cos{\phi} -mgR\cos(\phi - \theta)=0$

Note that the system is at rest at the beginning so the initial conditions are:

$\theta(0) = \phi(0) = \dot{\theta}(0) = \dot{\phi}(0)=0$

At $t=0$ applying the initial conditions in the above equations and simplifying, gives the following two equations:

$\ddot{\phi} = 4\ddot{\theta}$ $\ddot{\phi} - \ddot{\theta} = \frac{g}{R}$

Solving gives:

$\ddot{\phi} = \frac{4g}{3R}$ $\ddot{\theta} = \frac{g}{3R}$

Finally, the acceleration of A and B at $t=0$ is computed as follows:

$a_A = \sqrt{\ddot{x}_A(0)^2 + \ddot{y}_A(0)^2}$ $a_B = \sqrt{\ddot{x}_B(0)^2 + \ddot{y}_B(0)^2}$

Crunching out all derivatives and substituting all initial conditions are derived earlier gives:

$a_A = \frac{g\sqrt{2}}{3}$ $a_B = \frac{g\sqrt{10}}{3}$

Now, when the system finally comes to rest due to viscous friction, the system will be in its state of stable equilibrium. At this stage:

$\dot{\phi} = \dot{\theta} = \ddot{\phi} = \ddot{\theta}=0$

Substituting in Lagrange's equations gives:

$2\sin{\theta} -\cos{\theta} + \cos(\phi - \theta)=0$ $\cos(\phi - \theta)=0$ $\implies \tan{\theta} = \frac{1}{2}$ Finally:

$\boxed{\alpha = \frac{\sqrt{2}}{3}}$ $\boxed{\beta = \frac{\sqrt{10}}{3}}$ $\boxed{\gamma = \frac{1}{2}}$