Rinse and repeat ....
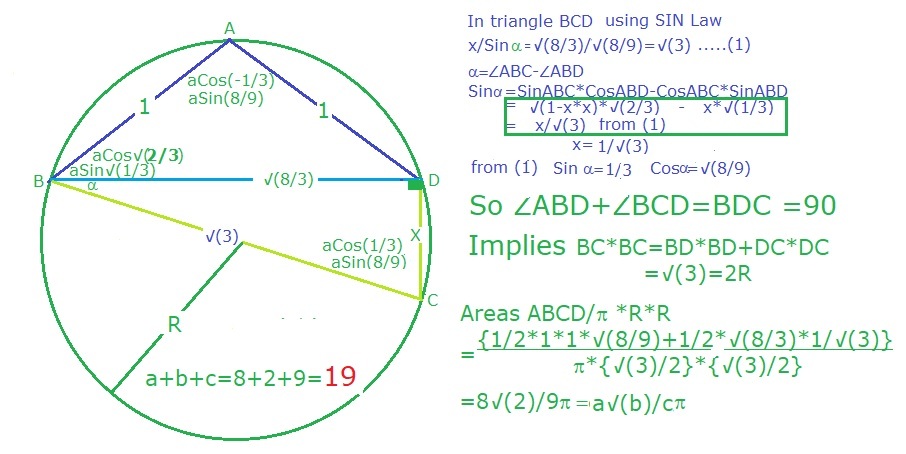
Suppose a cyclical quadrilateral A B C D is such that
(i) A B = A D = 1 ,
(ii) C D = cos ( ∠ A B C ) and
(iii) cos ( ∠ B A D ) = − 3 1 .
The ratio of the area of A B C D to the area of the circle in which it is inscribed can be expressed as c π a b , where a , c are positive coprime integers and b is a positive square-free integer.
Find a + b + c .
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Hi sir . Enjoyed solving this question but I have a small problem . While solving this question , I tried to tackle this question by creating cases of generality .
First I assumed BC to be equal to CD , I found that I was wrong right away .
Second I let angle DBC as 90 and solved . No output . Then I let angles ADC and ABC to be equal to 90 degrees and solved , no output . Then I let angle BDC = 90 degree since 3 x ≥ x , only then was I able to solve it .
Can you please tell me how angles BDC = 90 degree ? Sorry, but couldn't understand it from your solution .
Thanks for the same .
Log in to reply
I'm glad that you enjoyed working on the problem.
Taking a look at triangle Δ B C D in isolation, let C D = x be the base. Then C B = 3 x makes an angle ∠ B C D with C D . Since cos ( ∠ B C D ) = 3 1 , we know that when we "drop" a perpendicular from B to the line on which C D lies, it will intersect this line at D . This implies that ∠ B D C = 9 0 ∘ . Hope that makes sense. :)
Log in to reply
Thanks a lot sir !! In my hurry to solve the question , I missed out on a couple of things and ignored some basic facts and this being one of them . Yeah, haste makes waste .
Thanks again sir .
First, using the Cosine Law we have that
( B D ) 2 = ( A B ) 2 + ( A D ) 2 − 2 ∗ ( A B ) ( A D ) cos ( ∠ B A D ) =
2 − 2 ∗ ( − 3 1 ) = 3 8 ⟹ B D = 3 8 .
Now let C D = cos ( ∠ A B C ) = x . Since A B C D is cyclic we have that
cos ( ∠ A D C ) = − cos ( ∠ A B C ) = − x and
cos ( ∠ B C D ) = − cos ( ∠ B A D ) = 3 1 .
Nwxt, since Δ A B C and Δ A D C have chord A C in common, we can use the Cosine Law to set up the following equation:
1 2 + x 2 − 2 ( 1 ) ( x ) cos ( ∠ A D C ) = 1 2 + ( B C ) 2 − 2 ( 1 ) ( B C ) cos ( ∠ A B C )
⟹ 1 + x 2 − 2 x ∗ ( − x ) = 1 + ( B C ) 2 − 2 ( B C ) ( x )
⟹ ( B C ) 2 − 2 x ∗ ( B C ) − 3 x 2 = 0 ⟹ ( B C − 3 x ) ( B C + x ) = 0 .
Now since B C > 0 we have that B C = 3 x . But since the sides D C and B C are in the ratio x : 3 x ⟹ 1 : 3 and cos ( ∠ B C D ) = 3 1 we can conclude that Δ B C D is a right triangle with ∠ B D C = 9 0 ∘ . This implies that B C is a diameter of the circle in which A B C D is inscribed.
Using Pythagoras, we then have that
( B C ) 2 = ( C D ) 2 + ( B D ) 2 ⟹ 9 x 2 = x 2 + 3 8 ⟹ x = C D = 3 3 ,
as x > 0 , and so B C = 3 x = 3 .
So with these side lengths, we can apply the formula for the area of a cyclic quadrilateral, namely
( s − t ) ( s − u ) ( s − v ) ( s − w )
where t , u , v , w are the side lengths and s = 2 t + u + v + w .
With s = 2 1 + 1 + 3 3 + 3 = 1 + 3 2 3 the area calculation becomes
( 3 2 3 ) 2 ( 1 + 3 3 ) ( 1 − 3 3 ) = 3 2 2 .
The area of the circle is π ∗ ( 2 3 ) 2 = 4 3 π ,
so the desired ratio is 4 3 π 3 2 2 = 9 π 8 2 .
Thus a + b + c = 8 + 2 + 9 = 1 9 .