Rising water level
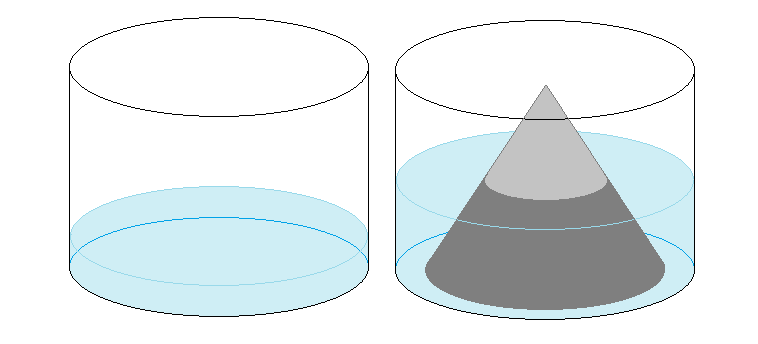
A cylindrical container with a base radius of and a height of has water in it to a depth of .
A steel cone with a base radius and a height of is placed inside.
What is the new depth of the water in ?
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The volume of water in both pictures is π ∗ 5 2 ∗ 1 . 7 1 = 4 2 . 7 5 π c m 3 .
If we call the depth to be found x , the second picture has the cone displacing water up to a frustum of height x .
The volume of this frustum is 3 1 π ∗ 4 2 ∗ 8 − 3 1 π ∗ ( 4 − 2 1 x ) 2 ∗ ( 8 − x ) = ( 1 2 1 x 3 − 2 x 2 − 9 x ) π
The volume of the water plus frustum must be equal to 2 5 π x
Setting the frustum as the difference between the two depth volumes gives the equation to be solved
1 2 1 x 3 − 2 x 2 − 9 x + 4 2 . 7 5 = 0
This cubic has extraneous solutions of x = 2 2 1 ± 1 5 5 . The solution of interest is exactly x = 3 c m