RL 11-22-2020
An exponentially decaying voltage source supplies an R L circuit as shown. At time t = 0 , there is no current in the inductor. What is the largest value of current in the circuit over all time?
Details and Assumptions:
1)
V
S
(
t
)
=
e
−
t
2)
R
=
L
=
1
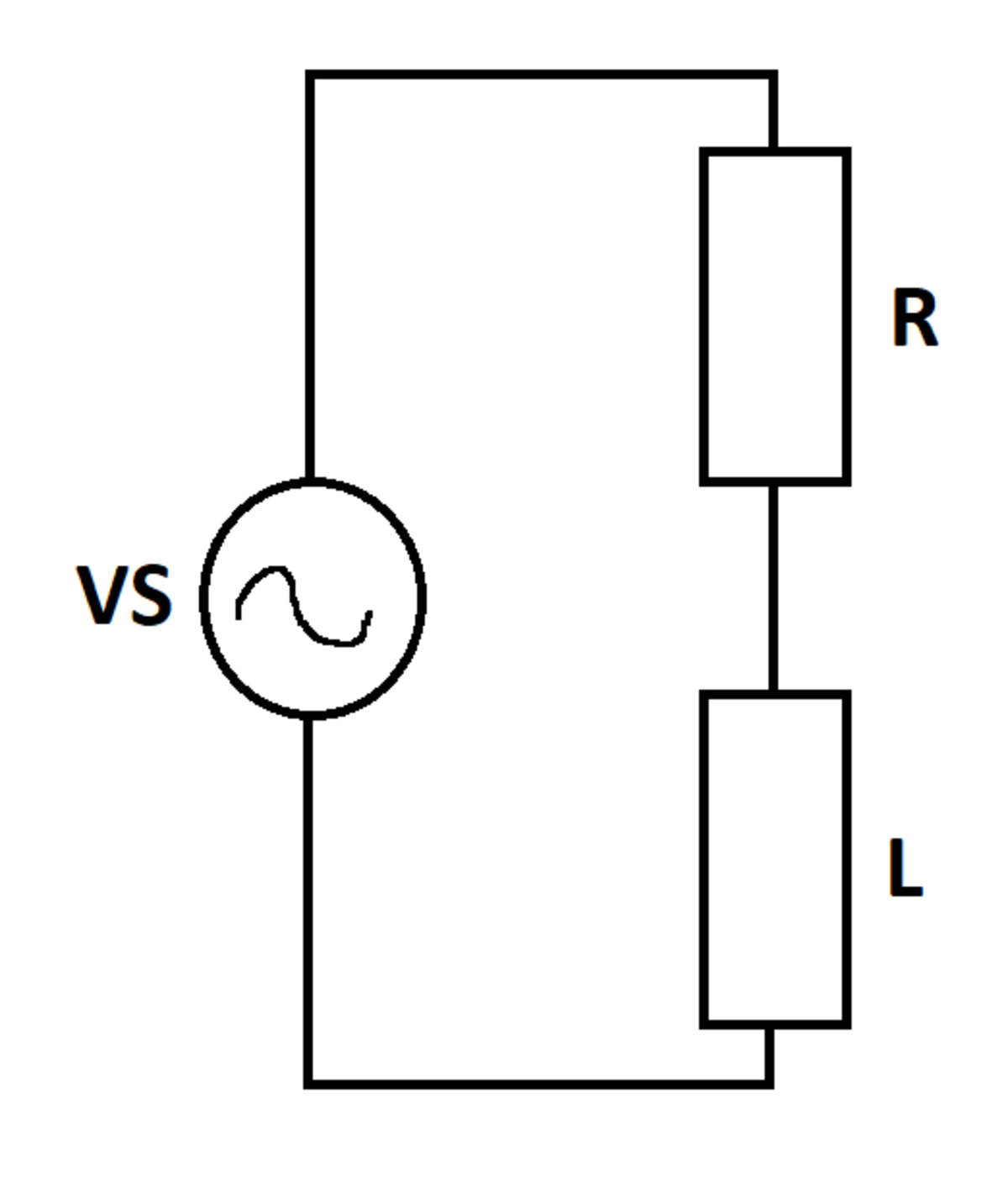
The answer is 0.3679.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let's take a Laplace Transform approach on this RL circuit. Per KVL, if the circuit be represented by:
L i ′ ( t ) + R i ( t ) = V S ( t ) ,
or i ′ ( t ) + i ( t ) = e − t , i ( 0 ) = 0
then the Laplace Transform yields:
[ s I ( s ) − i ( 0 ) ] + I ( s ) = s + 1 1 ;
or ( s + 1 ) I ( s ) = s + 1 1 ;
or I ( s ) = ( s + 1 ) 2 1 ;
or i ( t ) = t e − t . Taking the first derivative of i ( t ) equal to zero gives:
i ′ ( t ) = ( 1 − t ) e − t = 0 ⇒ t = 1
and the second derivative at t = 1 gives:
i ′ ′ ( t ) = ( t − 2 ) e − t ⇒ i ′ ′ ( 1 ) = − e − 1 < 0 (hence, a maximum over t ≥ 0 ).
Thus, i M A X = i ( 1 ) = e 1 amps.
We are asked to solve the differential equation:
I ˙ + I = e − t ; I ( 0 ) = 0 ⟹ e t I ˙ + e t I = 1 ⟹ d t d ( e t I ) = 1 ⟹ I = ( t + c ) e − t ∵ I ( 0 ) = 0 ⟹ c = 0 ⟹ I = t e − t
To compute the maximum value of current:
I ˙ = ( 1 − t ) e − t = 0 ⟹ t = 1
The second derivative check shows that:
I ¨ ( 1 ) = − e 1 < 0
Therefore, t = 1 corresponds to a maxima. Therefore, the maximum current occurs at t = 1 and its value is:
I m a x = I ( 1 ) = e 1