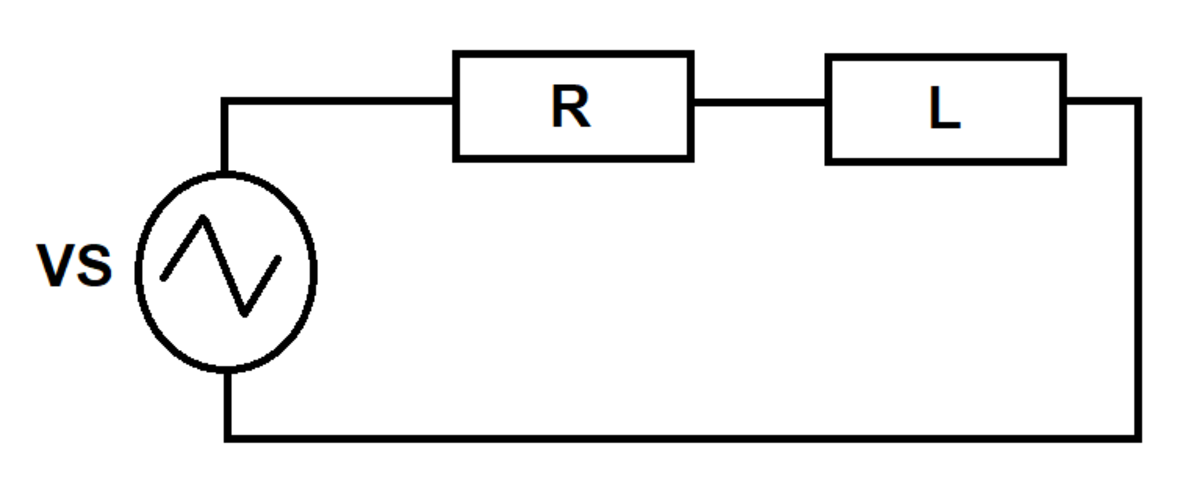
RL with Triangle Wave Source

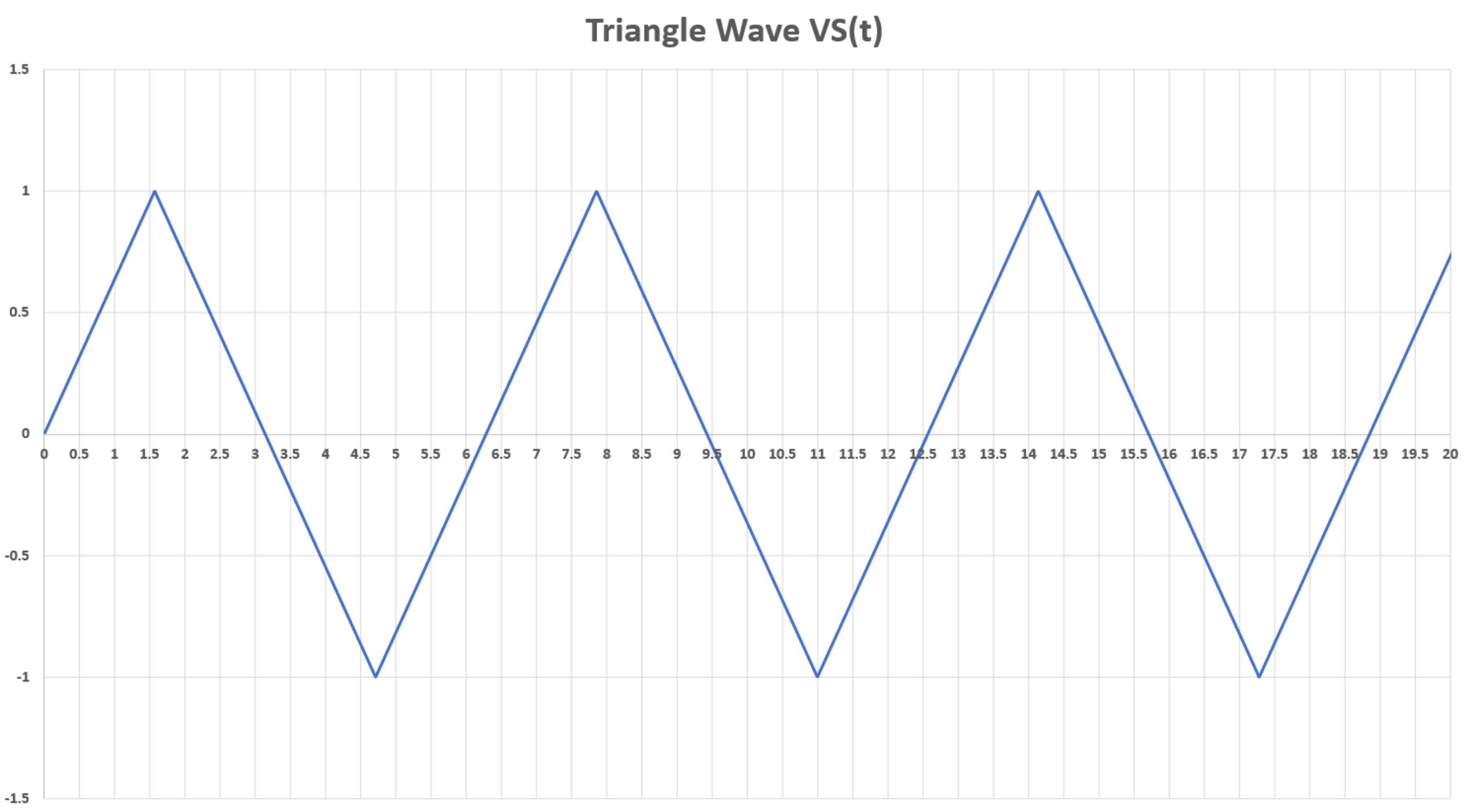
Electricity and Magnetism Level pending

A triangle wave voltage source $V_S(t)$ excites an $RL$ circuit as shown. The source voltage is zero at time $t = 0$ . It is bounded between $-1$ and $+1$ volts, and it has a rate of change of $\frac{2}{\pi}$ volts per second. Whenever the source voltage gets to either $-1$ or $+1$ , its rate of change (slope) is multiplied by $-1$ . See the attached image.

At time $t = 0$ , there is no current in the circuit. In steady state, after initial transients have died out, what is the peak instantaneous value of the current?

Bonus: If $V_S(t)$ was a pure sine wave with the same peak value and time period as the source signal in this problem, what would the peak steady state current magnitude be? Why is the current magnitude smaller with a triangle wave input?

Details and Assumptions:
1) $R = 0.1$
2) $L = 1$
3) All quantities are in standard $SI$ units

The answer is 0.782.

1 solution

Karan Chatrath
Dec 27, 2020

This is a good one. First, the triangular wave signal's equation was computed. It was found to be as follows:

$V_S(t)= \begin{cases} \frac{2t}{\pi}-4n & 2\pi n \leq t < 2\pi n + \frac{\pi}{2}\\ - \frac{2t}{\pi}+4n+2 & 2\pi n + \frac{\pi}{2} \leq t < 2\pi n + \frac{3\pi}{2} \\ \frac{2t}{\pi}-4n-4 & 2\pi n + \frac{3\pi}{2} \leq t < 2\pi n \end{cases}$

$n =\biggr \lfloor \frac{t}{2 \pi}\biggr \rfloor$

Having obtained $V_S(t)$ the circuit equation is:

$L\dot{I} + IR = V_S(t)$ $I(0) = 0$

I have avoided doing this analytically. So numerical integration takes care of the rest. The following plot is hopefully illustrative:

If one looks at the area under the magnitude of the sources, that under the sine wave source is higher than the triangle wave source. This area can be thought of as a quantity proportional to the total energy delivered by the source per unit current (I am unsure of this proportionality). Thus, the energy delivered by the sine source is higher. I speculate that this is the reason behind the current magnitude being higher for the sine case. I may be wrong here, though.

Thanks for the solution. I think your point about the larger effective magnitude of the sine wave plays a role here. It is also instructive to think of the triangle wave in terms of a Fourier series. The triangle wave can be represented by a sum of sine waves at progressively higher frequencies. As the frequency goes up, the inductor impedance seen at that frequency increases. So the higher-harmonic source voltage components don't really translate into higher-harmonic current components. In terms of current as an output vs. voltage as an input, the circuit is basically a low-pass filter. I suspect that this also plays a role in making the current smaller than in the sinusoidal excitation case.

Steven Chase - 5 months, 2 weeks ago

The Fourier series' argument is interesting. It would be a good exercise to see the contribution of individual frequency components to the solution. I'll try this myself and maybe post a follow-up.

Karan Chatrath - 5 months, 2 weeks ago

RL with Triangle Wave Source

The answer is 0.782.

1 solution

0 pending reports