RLC 11-30-2020
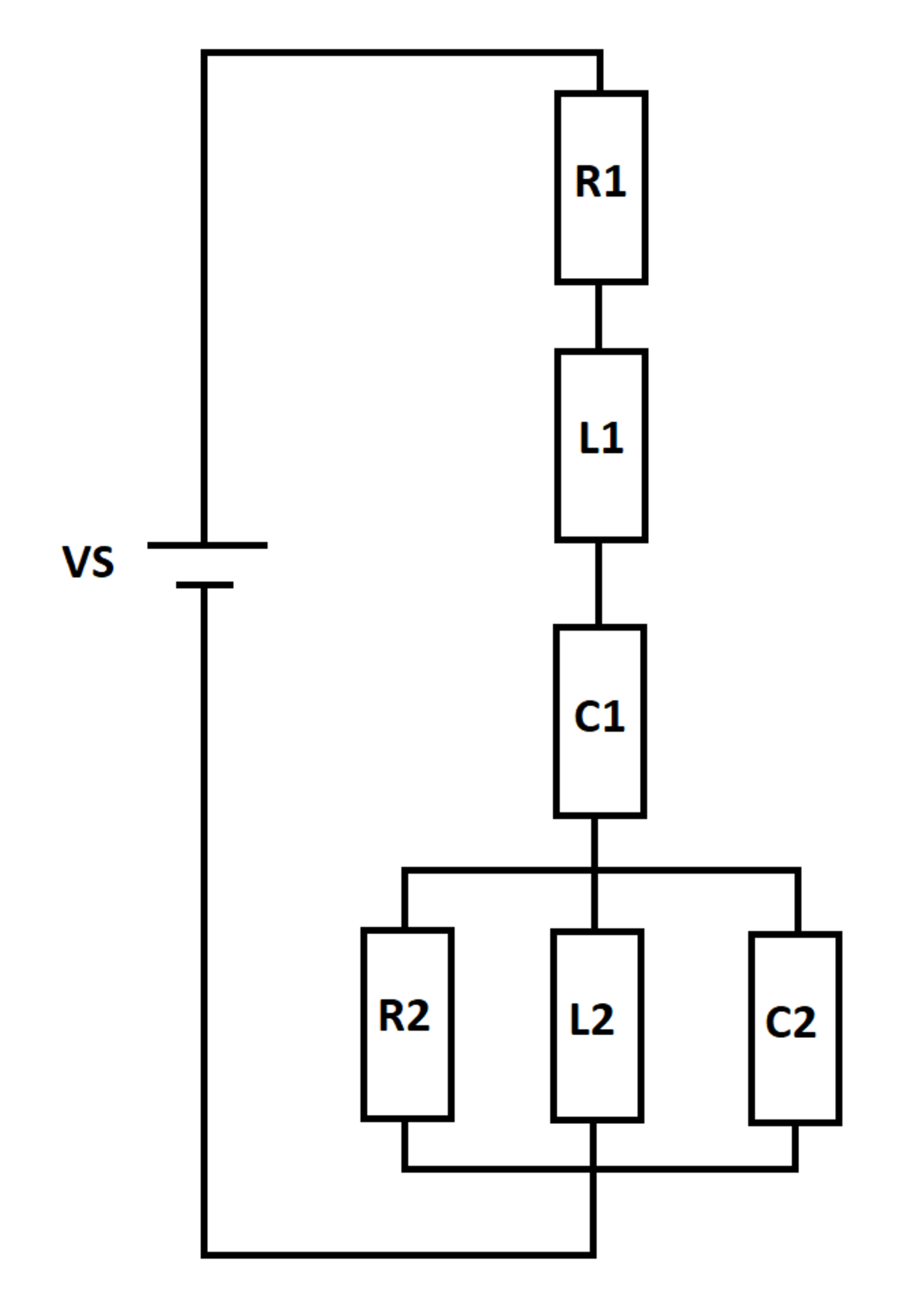
A voltage source supplies an network as shown. At time , the inductors and capacitors are de-energized. How much energy is dissipated in resistor from to ?
Details and Assumptions:
1)
2)
3)
All quantities are in the appropriate standard
units
The answer is 37.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I − S o u r c e C u r r e n t ; Q − C 1 c h a r g e ; I 1 − R 2 c u r r e n t I 2 − L 2 c u r r e n t ; I 3 − C 2 c u r r e n t ; Q 3 − C 2 c h a r g e
C i r c u i t E q u a t i o n s : − V S + I R 1 + L 1 I ˙ + C 1 Q + I 1 R 2 = 0 Q ˙ = I I 1 R 2 = L 2 I ˙ 2 I 1 R 2 = C 2 Q 3 Q ˙ 3 = I 3 I = I 1 + I 2 + I 3
R e a r r a n g i n g e q u a t i o n s t o s t a t e s p a c e f o r m : ⎣ ⎢ ⎢ ⎡ I ˙ Q ˙ Q ˙ 3 I ˙ 2 ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ − 1 1 1 0 − 1 0 0 0 − 1 0 − 1 1 0 0 − 1 0 ⎦ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎡ I Q Q 3 I 2 ⎦ ⎥ ⎥ ⎤ + ⎣ ⎢ ⎢ ⎡ 1 0 0 0 ⎦ ⎥ ⎥ ⎤ V s ⟹ x ˙ = A x + B V s ⟹ I = [ 1 0 0 0 ] x x ( 0 ) = ⎣ ⎢ ⎢ ⎡ 0 0 0 0 ⎦ ⎥ ⎥ ⎤
O D E s y s t e m s o l v e d u s i n g I m p l i c i t E u l e r : x ( k + 1 ) = ( I − δ t A ) − 1 ( x ( k ) + δ t B V s )
H e a t D i s s i p a t i o n : H = ∫ 0 ∞ R 1 I 2 d t ≈ 3 7 . 5