RLC (5-10-2020)
A DC voltage source excites an RLC circuit as shown below. At time , the inductor and capacitor are de-energized. How much energy is dissipated in the resistor from to ?
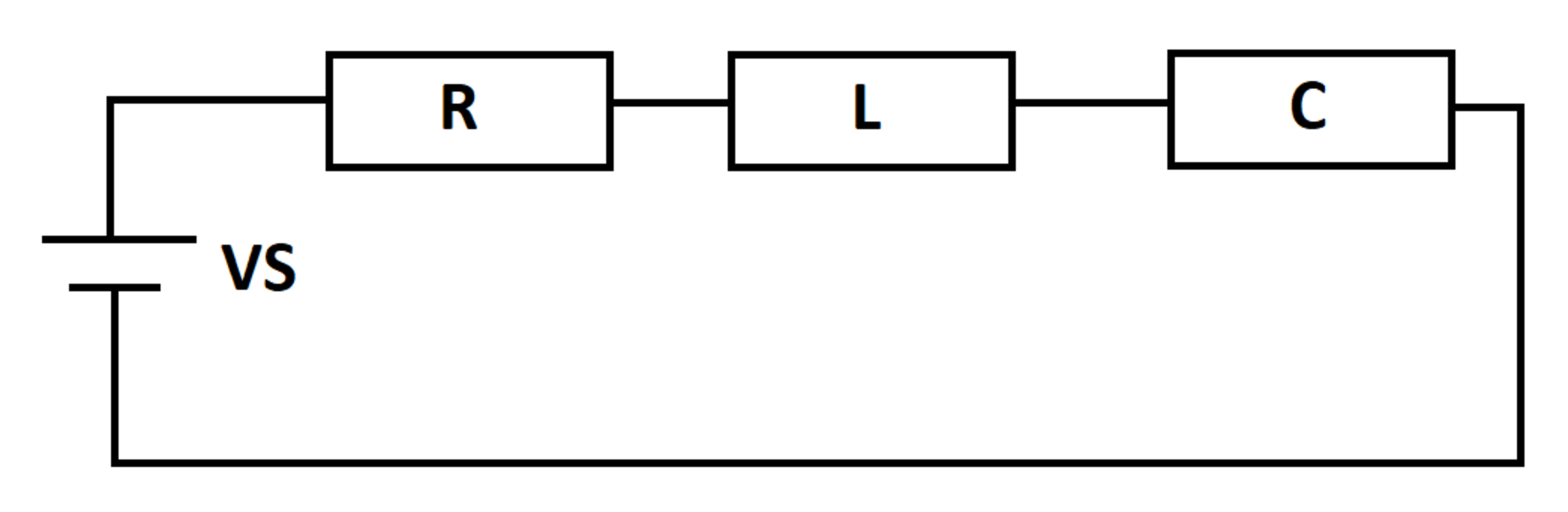
Details and Assumptions:
1)
2)
3)
The answer is 50.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
F u n P r o b l e m . I will be very happy if you continue this series.
The basic equations are V s − I R − L d T d I − c q = 0
After substituting values 1 0 − 4 I − d T d I − q = 0
As we know I = d T d q = q ˙ After substituting this 1 0 − 0 . 2 5 q ˙ − q ¨ − q = 0 Solving this double differential equation leads to q ( t ) = c 1 e − 0 . 1 2 5 t s i n ( 0 . 9 9 2 1 5 7 t ) + c 2 e − 0 . 1 2 5 t c o s ( 0 . 9 9 2 1 5 7 ) + 1 0 where c 1 and c 2 are arbitrary constant.
Using this q ( 0 ) = 0 q ˙ ( 0 ) = 0 we can find the value of c 1 and c 2 easily.
After that we will reach q ( t ) = − 1 . 2 5 9 8 8 1 2 5 e − 0 . 1 2 5 t s i n ( 0 . 9 9 2 1 5 7 t ) − 1 0 e − 0 . 1 2 5 t c o s ( 0 . 9 9 2 1 5 7 ) + 1 0 Differentiate q ( t ) to get I ( t ) I ( t ) = 1 0 . 0 7 9 1 e − 0 . 1 2 5 t s i n ( 0 . 9 9 2 1 5 7 t ) Heat dissipated H = ∫ 0 ∞ ( I ( t ) ) 2 R d t H = 5 0 . 0 0 0 5