RLC 6-14-2020
In the RLC circuit shown below, the capacitors and inductor are de-energized at time t = 0 . From then on, power flows out of the DC voltage source for most of the time, but for a brief time, power flows into the source.
What is the largest instantaneous power flowing into the source?
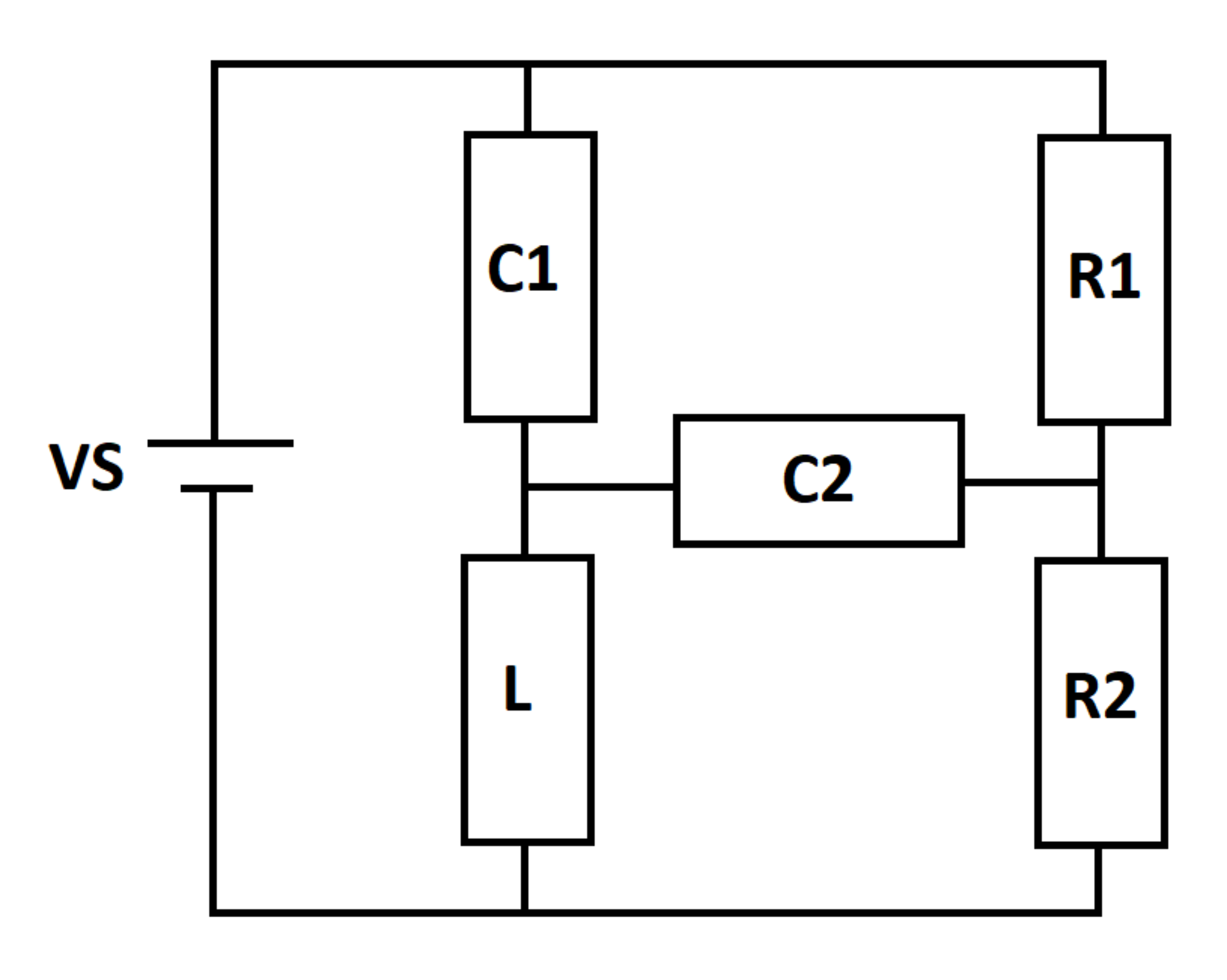
Details and Assumptions:
1)
V
S
=
1
0
2)
R
1
=
4
3)
R
2
=
1
4)
C
1
=
1
5)
C
2
=
1
6)
L
=
1
7)
Give your answer as a positive number
The answer is 12.72.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
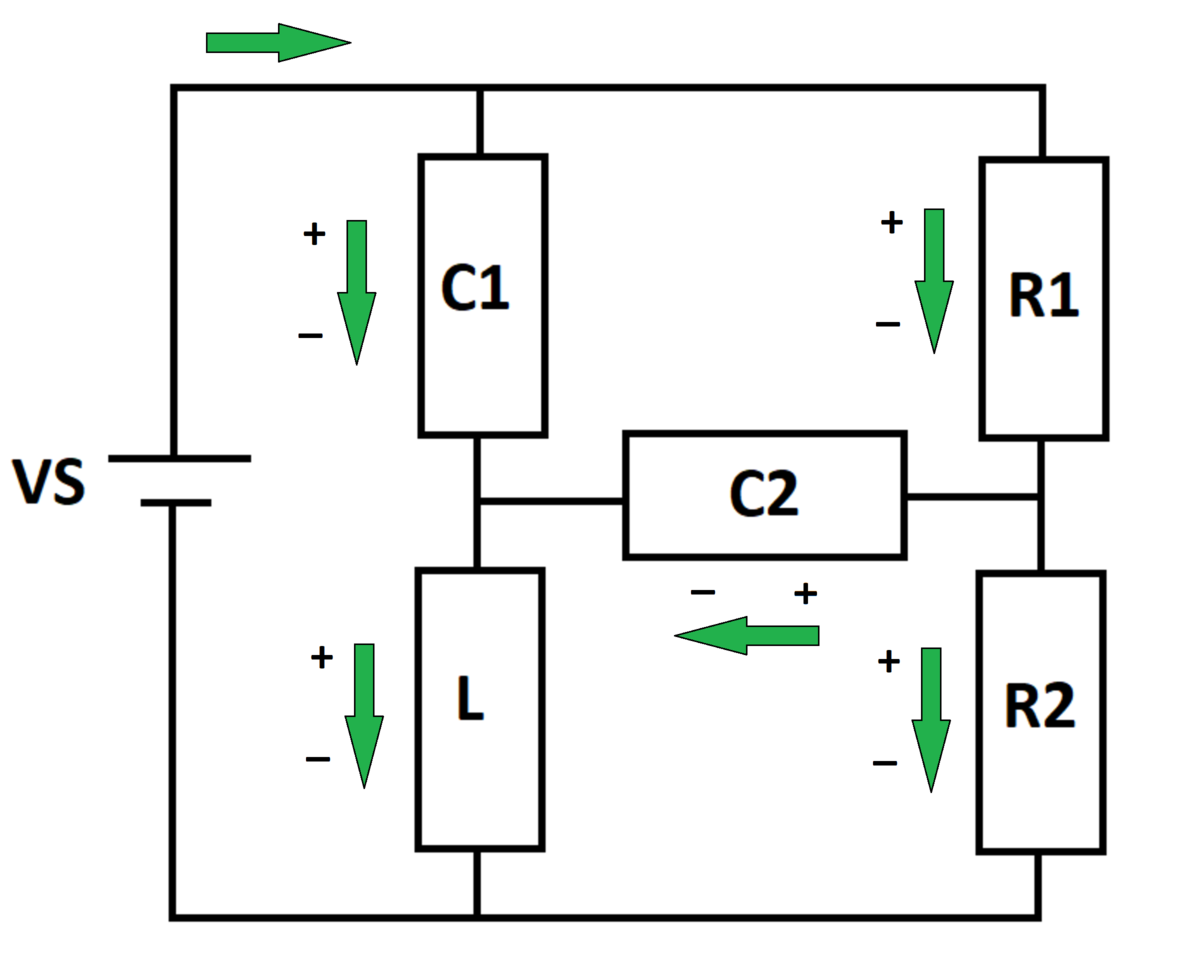
The state variables are the capacitor voltages and the inductor currents. Write the fundamental equations for these elements:
V L = L I ˙ L I C 1 = C 1 V ˙ C 1 I C 2 = C 2 V ˙ C 2
Now write the left sides in terms of state variables (with some intermediate quantities to aid in calculating):
V L = V S − V C 1 = L I ˙ L I R 1 = R 1 V C 1 − V C 2 I R 2 = R 2 V S − V C 1 + V C 2 I C 2 = I R 1 − I R 2 I C 1 = I L − I C 2 I C 1 = C 1 V ˙ C 1 I C 2 = C 2 V ˙ C 2
Solve for the derivatives and numerically integrate. The source current (flowing out of the source) is:
I S = I C 1 + I R 1
The power flowing out of the source is:
P S = V S I S
If P S > 0 , power is flowing out of the source. If P S < 0 , power is flowing into the source. So find the largest negative value of P S , and the absolute value of that is the answer.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 |
|
@Steven Chase I want to say sorry if you feel any inconvenience with me.
Source current: I
Charge on C 1 = Q 1
Charge on C 2 = Q 2
Circuit equations:
I = I R 1 + I C 1 I R 1 = I C 2 + I R 2 I L = I C 1 + I C 2
Q ˙ 1 = I C 1 Q ˙ 2 = I C 2
− V S + C 1 Q 1 + L I ˙ L = 0 I R 1 R 1 + C 2 Q 2 = C 1 Q 1 I R 2 R 2 = C 2 Q 2 + L I ˙ L
Q 1 ( 0 ) = I L ( 0 ) = Q 2 ( 0 ) = 0
I would have preferred to obtain the closed-form solution for the source current using Laplace transforms but the online calculator yields no result. So I went the usual numerical route. The variation of power provided by the source with time is:
It can be seen that at a certain interval, the power provided by the source becomes negative which indicates that power flows into the source. The maximum value of the power inflow to the source is the minimum value of the function plotted above. The answer is ≈ 1 2 . 7 2