RLC Bridge (2-6-2021)
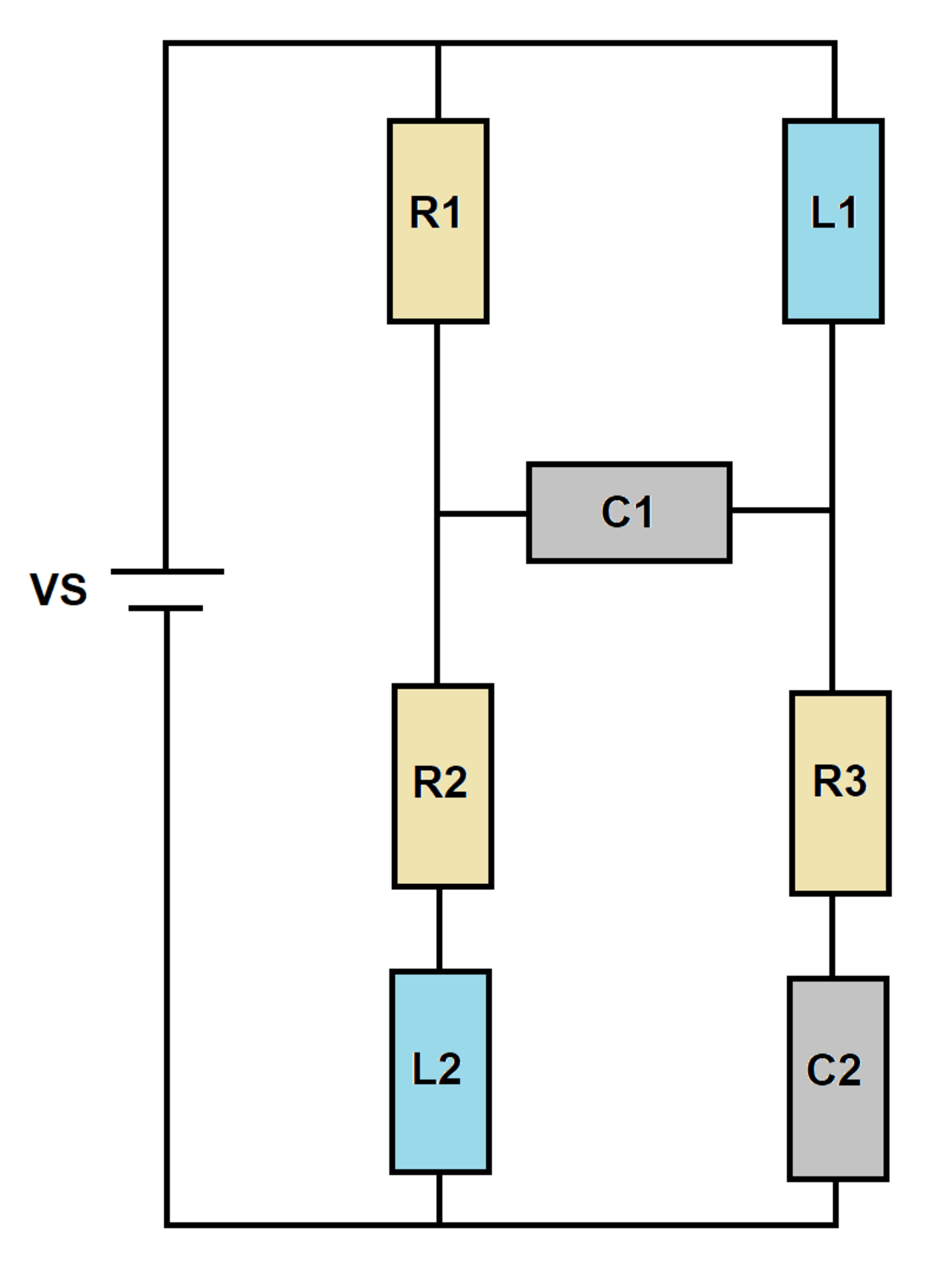
A voltage source supplies an circuit as shown below. At time , the capacitors and inductors are de-energized. is the current flowing out of the source.
Let and be the values of at and respectively. Let and be the largest and smallest values of between and .
Enter your answer as the product of , , , and .
Details and Assumptions:
1)
2)
The answer is 705.02.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Been a while since I had a go at one of these circuit problems. This was fun.
Circuit equations as per Kirchoff's laws:
Q ˙ C 1 = I C 1 … ( 1 ) Q ˙ C 2 = I C 2 … ( 2 ) I S = I L 1 + I R 1 … ( 3 ) I L 1 = I C 1 + I C 2 … ( 4 ) I L 2 = I R 1 + I C 1 … ( 5 ) L 1 I ˙ L 1 + R 3 I C 2 + C 2 Q C 2 = V S … ( 6 ) L 1 I ˙ L 1 + C 1 Q C 1 = R 1 I R 1 … ( 7 ) R 3 I C 2 + C 2 Q C 2 = R 2 I L 2 + L 2 I ˙ L 2 + C 1 Q C 1 … ( 8 )
Now eliminating I R 1 in (7) using (3):
L 1 I ˙ L 1 + C 1 Q C 1 = R 1 ( I L 2 − Q ˙ C 1 ) … ( 9 )
(2) can also be written as:
Q ˙ C 1 + Q ˙ C 2 = I L 1
Using (2), (6), (8) and (9) to construct a system of ODE's in matrix form gives:
⎣ ⎢ ⎢ ⎡ L 1 L 1 0 0 0 0 − L 2 0 0 R 1 0 1 R 3 0 R 3 1 ⎦ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎡ I ˙ L 1 I ˙ L 2 Q ˙ C 1 Q ˙ C 2 ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ 0 0 0 1 0 R 1 R 2 0 0 − 1 / C 1 1 / C 1 0 − 1 / C 2 0 1 / C 2 0 ⎦ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎡ I L 1 I L 2 Q C 1 Q C 2 ⎦ ⎥ ⎥ ⎤ + ⎣ ⎢ ⎢ ⎡ 1 0 0 0 ⎦ ⎥ ⎥ ⎤ V S Let:
A = ⎣ ⎢ ⎢ ⎡ L 1 L 1 0 0 0 0 − L 2 0 0 R 1 0 1 R 3 0 R 3 1 ⎦ ⎥ ⎥ ⎤ B = ⎣ ⎢ ⎢ ⎡ 0 0 0 1 0 R 1 R 2 0 0 − 1 / C 1 1 / C 1 0 − 1 / C 2 0 1 / C 2 0 ⎦ ⎥ ⎥ ⎤ C = ⎣ ⎢ ⎢ ⎡ 1 0 0 0 ⎦ ⎥ ⎥ ⎤ x = ⎣ ⎢ ⎢ ⎡ I L 1 I L 2 Q C 1 Q C 2 ⎦ ⎥ ⎥ ⎤
⟹ A x ˙ = B x + C V S x ( 0 ) = ⎣ ⎢ ⎢ ⎡ 0 0 0 0 ⎦ ⎥ ⎥ ⎤
Explicit Euler numerical integration yields:
x k + 1 = x k + δ t ( A − 1 ( B x k + C V S ) )
Iterating this in a loop using a short script of code yields the required answer. To get I S , a linear combination of appropriate states and their derivatives need to be taken keeping in mind equation (3). For a step size of 1 0 − 5 s e c , the answer I get is 7 0 4 . 9 5 .