RLC Circuit Current Determination

Electricity and Magnetism Level 4

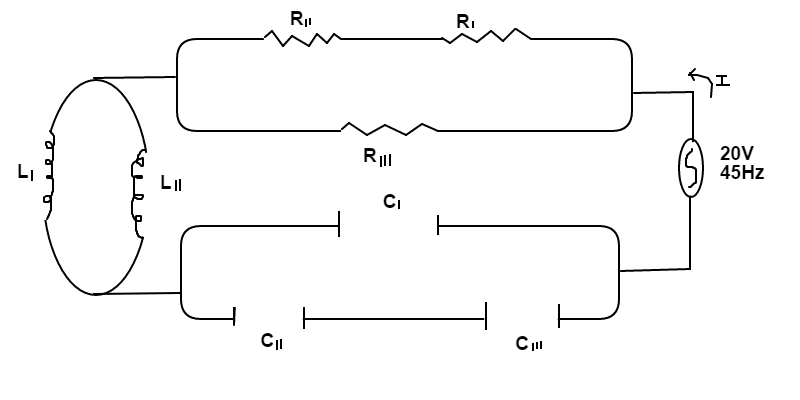
An RLC circuit was prepared with an AC power supply that has a voltage ( V s V_s ) of 20 V 20V and a frequency ( f f ) of 45 H z 45Hz . The circuit consists of resistors ( R R ), capacitors ( C C ), and inductors ( L L ). The resistor resistances are as follows: R I = 2 Ω R_{I}=2Ω , R I I = 4 Ω R_{II}=4Ω , and R I I I = 3 Ω R_{III}=3Ω . The inductors have the following inductances: L I = 4 π H L_{I}=\frac{4}{\pi}H and L I I = 12 π H L_{II}=\frac{12}{\pi}H . The capacitors have these capacitances: C I = 30 π μ F C_{I}=\frac{30}{\pi}μF , C I I = 90 π μ F C_{II}=\frac{90}{\pi}μF , and C I I I = 180 π μ F C_{III}=\frac{180}{\pi}μF .

What is the peak current ( I I ) of this circuit in m A mA ?

David's Electricity Set
116 121 136 141

David Hontz by David Hontz , 26, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

David Hontz
May 28, 2016

R I , I I = R I + R I I = 2 + 4 = 6 Ω R c i r c u i t = ( 1 R I I I + 1 R I , I I ) − 1 = ( 1 3 + 1 6 ) − 1 = ( 1 2 ) − 1 = 2 Ω R_{I,II}=R_I+R_{II}=2+4=6Ω \\ R_{circuit}=(\frac{1}{R_{III}}+\frac{1}{R_{I,II}})^{-1}=(\frac{1}{3}+\frac{1}{6})^{-1}=(\frac{1}{2})^{-1}=\boxed{2Ω}

L c i r c u i t = ( 1 L I + 1 L I I ) − 1 = ( π 4 + π 12 ) − 1 = ( π 3 ) − 1 = 3 π H L_{circuit}=(\frac{1}{L_I}+\frac{1}{L_{II}})^{-1}=(\frac{\pi}{4}+\frac{\pi}{12})^{-1}=(\frac{\pi}{3})^{-1}=\boxed{\frac{3}{\pi}H}

C I I , I I I = ( 1 C I I + 1 C I I I ) − 1 = ( π 90 + π 180 ) − 1 = ( π 60 ) − 1 = 60 π μ F C c i r c u i t = C I + C I I , I I I = 30 π + 60 π = 90 π μ F C_{II,III}=(\frac{1}{C_{II}}+\frac{1}{C_{III}})^{-1}=(\frac{\pi}{90}+\frac{\pi}{180})^{-1}=(\frac{\pi}{60})^{-1}=\frac{60}{\pi}μF \\ C_{circuit}=C_I+C_{II,III}=\frac{30}{\pi} + \frac{60}{\pi} = \boxed{\frac{90}{\pi}μF}

X L = 2 π f L c i r c u i t = 2 π ( 45 H z ) ( 3 π H ) = 270 Ω X C = 1 2 π f C c i r c u i t = 1 2 π ( 45 H z ) ( 90 π × 1 0 − 6 F ) = 10000 81 Ω Z = R 2 + ( X L − X C ) 2 = 2 2 + ( 270 − 10000 81 ) 2 = 2 35230786 81 Ω X_L=2\pi f L_{circuit}=2\pi (45Hz)(\frac{3}{\pi}H)=\boxed{270Ω} \\ X_C= \frac{1}{2\pi f C_{circuit}}=\frac{1}{2 \pi (45Hz) (\frac{90}{\pi} \times 10^{-6}F)} =\boxed{\frac{10000}{81}Ω} \\ Z=\sqrt{R^2 + (X_L-X_C)^2}=\sqrt{2^2 + (270- \frac{10000}{81})^2}=\boxed{\frac{2 \sqrt{35230786}}{81}Ω}

I = 20 V 2 35230786 81 Ω = 405 2 17615393 ≈ 0.136 A = 136 m A ⇐ A n s w e r I = \frac{20V}{\frac{2 \sqrt{35230786}}{81}Ω} =405 \sqrt{\frac{2}{17615393}} \approx 0.136A = \boxed{136mA} \Leftarrow Answer

3 Helpful 0 Interesting 0 Brilliant 0 Confused

When you see 2 35230786 81 \frac {2\sqrt{35230786}}{81} , you'd think you've done something wrong somewhere. :P

Sharky Kesa - 5 years ago

Log in to reply

very true, I was clicking the answer having very heavy fingers.

Abhinav Jha - 5 years ago

This is unfair.No battery produces an ac current.I spend a lot of time trying to do it through DC supply.

Riju Kushwaha - 5 years ago

Log in to reply

Yeah, the image might mislead you into using DC, may be the battery should be changed. Anyway, the problem states that the voltage has certain frequency so it should be obvious that it is an AC circuit.

Erasmo Hinojosa - 5 years ago

for peak current you should multiply underroot 2 to your answer.as voltage provided are rms values otherwise stated.

AYUSH JAIN - 4 years, 9 months ago

This is wrong. When nothing is given you take RMS as 20.

Swapnil Vatsal - 3 years, 9 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...