RLC Conceptual Question
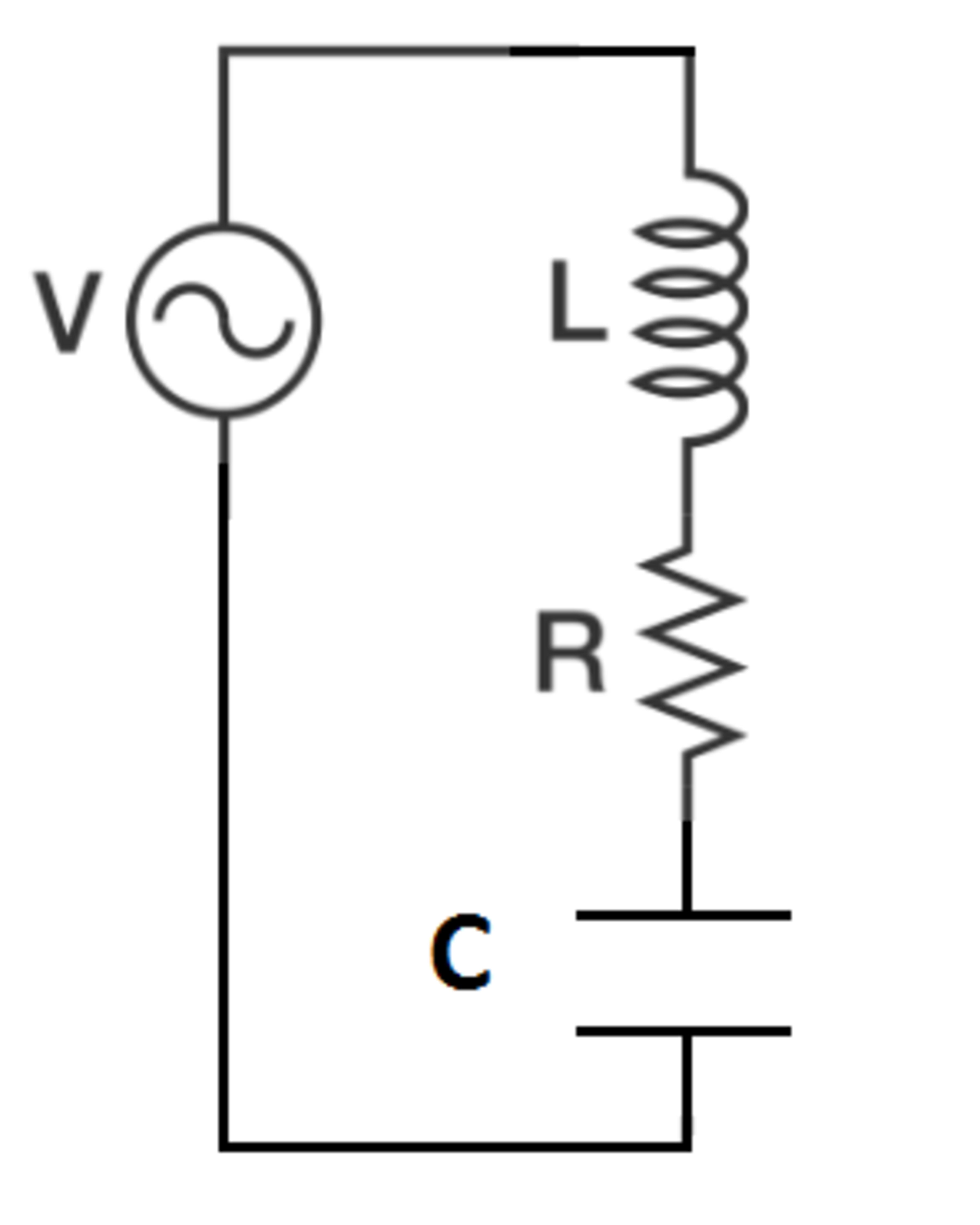
Consider a series RLC (resistive-inductive-capacitive) circuit driven by an ideal sinusoidal AC voltage source.
Can the voltage across the inductor change discontinuously (such as a step change)?
Note: Assume that infinite voltages and / or currents are impossible.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The voltage across an inductor CAN, in principle, change discontinuously. However, the presence of the other circuit elements constrains its behavior. The logic is as follows:
1) The source voltage cannot change discontinuously
2) If the voltage across the inductor changes discontinuously, the voltage across the RC series combination must also.
There are three ways for the voltage across the RC series combination to change discontinuously:
a) V R changes discontinuously but V C does not. This implies that the current through the resistor changes discontinuously. Because this is a series circuit, the current through the inductor would have to change discontinuously, which is by definition impossible.
b) V C changes discontinuously but V R does not. This is impossible by definition.
c) V R and V C both change discontinuously. This poses the same problems as in (a) and (b)
Therefore, the other circuit elements constrain the inductor so that its voltage cannot change discontinuously.