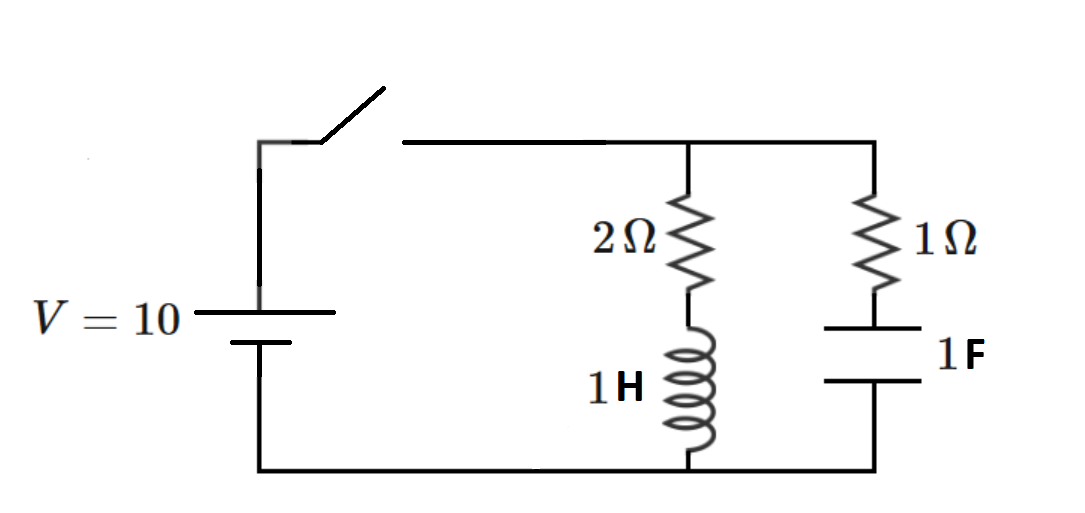
RLC DC Transient
The RLC circuit below is excited by a DC voltage source through a switch which is initially open. Prior to switch closing, the inductor and the capacitor are de-energized.
The switch closes at time . Let be the current flowing out of the voltage source, and let be the current flowing out of the voltage source as the elapsed time approaches infinity (representing DC steady-state).
Determine the following integral:
The answer is 7.4752.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Here's a quick and dirty solution:
1) at t = 0 , close the switch, no current flows in the inductor, since it takes time to get the magnetic field built up, maximum current flow in the capacitor, but no potential across it. This current is 10A by inspection.
2) After a long time, the only current that flows is in the inductor branch, so that's 1 0 V / 2 Ω = 5 A by inspection.
3) For all other times, the current in the inductor branch increases exponentially to the final current of 5A, so it must be I L = 5 − 5 e − L R t = 5 − 5 e − 2 t .
4) For all other times, the current in the capacitor branch decreases exponentially to the final current of 0, so it must be I C = 1 0 e − R C t = 1 0 e − t
5) To find the integral in question, add up the currents and integrate:
∫ 0 6 ( I S ( t ) − I S ∞ ) d t = ∫ 0 6 5 − 5 e − 2 t + 1 0 e − t − 5 d t = 2 5 e − 2 t − 1 0 e − t ∣ ∣ 0 6 = 2 5 e − 1 2 − 1 0 e − 6 + 7 . 5 ≈ 7 . 4 7 5 2