RLC H-Bridge
A DC voltage source feeds an RLC H-Bridge circuit through a switch. The switch is initially open, and the inductor and capacitor are initially de-energized.
By inspection, when the switch closes at time t = 0 , the current flowing out of the source is 1 0 amps. And the current flowing out of the source approaches 5 amps as the elapsed time goes toward infinity.
But the minimum source current during the transient is slightly less than 5 amps. If the minimum source current is I S m i n , give your answer as ⌊ 1 0 0 0 I S m i n ⌋ .
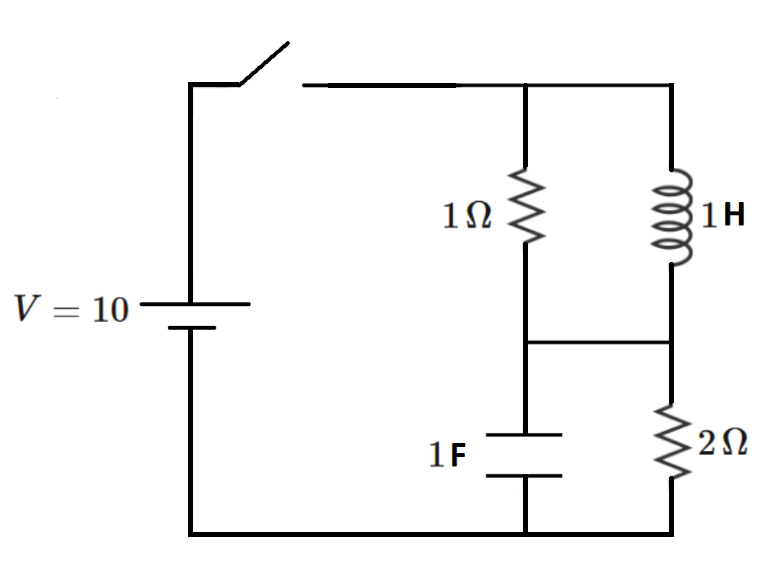
The answer is 4858.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Thanks for the solution. I hadn't seen a generalized inverse transformator utility until now
Log in to reply
I had long forgotten this Laplace thing, but looked it up because you were putting out problems with step function excitations ("close the switch"). It was fun to re-learn it after so many years. (BTW, by posting a bunch of excellent problems, you made me break my promise of not writing more solutions.)
Log in to reply
Glad you enjoyed it. I do hope you stick around, at least a bit.
Also, I assume you meant 4.8583 as the minimum, instead of 4.3583
Corrected.
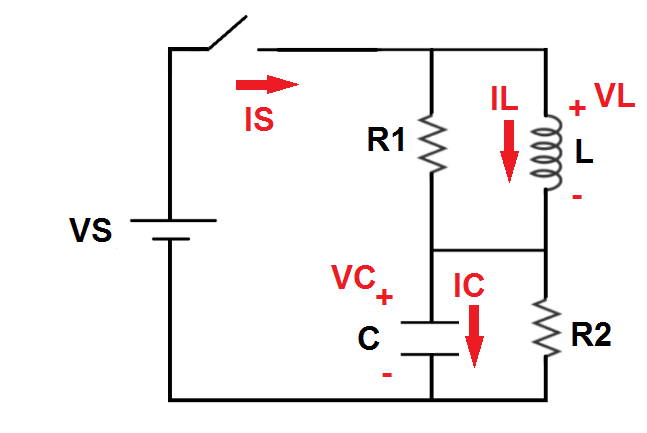
I will use the state space approach, combined with numerical integration. We want to solve for the inductor current and the capacitor voltage as state variables, and calculate the source current as a function of those. The idea is to express the time derivatives of the state variables as functions of the state variables and forcing function.
State-space expression for the inductor current:
V L = L I L ˙ V S − V C = L I L ˙ I L ˙ = L V S − V C
Expression for source current (note that this includes both state variables):
I S = I L + I R 1 I S = I L + R 1 V S − V C
State-space expression for the capacitor voltage:
I C = C V C ˙ I S − I R 2 = C V C ˙ I S − R 2 V C = C V C ˙ V C ˙ = C I S − V C / R 2
Numerical integration yields the following time plot for the source current. The current dips down to about 4.858.
Labeling the legs of the H 1 through 4, and assuming a potential V at the centre of the H we get the following information:
- Upper left : 1 0 − V = I 1 (resistor of 1Ω)
- Upper right: : 1 0 − V = I 2 ˙ (selfinductance of 1H)
- Lower left : V = ∫ I 3 d t (capacitor of 1C)
- Lower right : V = 2 I 4 (resistor of 2Ω)
Combining 1. and 2. we get I 1 = I 2 ˙ . Combining 3. and 4. we get I 3 = 2 I 4 ˙ .
Observe that the same current runs through the upper and lower half of the H:
I
1
+
I
2
=
I
3
+
I
4
.
Using the above results write this as
I
2
˙
+
I
2
=
2
I
4
˙
+
I
4
Observe that voltages add up:
1
0
=
V
1
+
V
4
=
I
1
R
1
+
I
4
R
4
=
I
1
⋅
1
+
I
4
⋅
2
so
I
1
=
1
0
−
2
I
4
and hence
2
I
4
=
1
0
−
I
2
˙
Use this to arrive at this differential equation:
2
I
2
¨
+
3
I
2
˙
+
2
I
2
=
1
0
which has the general solution:
I 2 ( t ) = ( a sin 4 7 t + b cos 4 7 t ) e 4 − 3 t + 5
I 2 ˙ = ( ( − 4 3 a − 4 7 b ) sin 4 7 t + ( − 4 3 b + 4 7 a ) cos 4 7 t ) e 4 − 3 t
This is just the current through the solenoid. To get the total current I, we use I = I 1 + I 2 = I 2 ˙ + I 2 to find I ( t ) = ( ( 4 a − 4 7 b ) sin 4 7 t + ( 4 b + 4 7 a ) cos 4 7 t ) e 4 − 3 t + 5
Because at time
t
=
0
no current runs through the selfinductance,
I
2
(
0
)
=
0
and hence
b
=
−
5
.
And since
I
(
0
)
=
1
0
, we see that
4
b
+
4
7
a
+
5
=
1
0
and hence
a
=
7
2
5
. We now know the total current I as a function of time:
I ( t ) = ( 7 1 5 7 sin 4 7 t + 5 cos 4 7 t ) e 4 − 3 t + 5
Now we look for the minima of I(t). Its time derivative
I
˙
(
t
)
=
7
−
2
0
7
sin
4
7
t
e
4
−
3
t
has zeros at
t
=
7
4
π
n
.
The first minimum after closing the switch has
I
(
7
4
π
)
=
5
(
1
−
e
7
−
3
π
)
=
4
.
8
5
8
1
.
.
.
We are going to use s-domain analysis and Laplace transformation. (Roughly speaking, s corresponds to j ω , where j = − 1 .) The impedance of the circuit is Z = 1 + s s + 1 + 2 s 2 . The admittance is Y = 1 / Z . The Laplace transform of the unit step function is 1 / s ; for a 10V source it is 1 0 / s . The time dependent current is the inverse Laplace transform of
s 1 0 Y = s ( 1 + s s + 1 + 2 s 2 ) 1 0
Feeding this function to an inverse Laplace transformator (e.g. here ) we get
i ( t ) = 1 0 [ 2 1 + ( 1 4 3 7 sin α t + 2 1 cos α t ) e − β t ]
where α = 4 7 and β = 4 3
Graphing the function yields a minimum value of 4.8583 around the time of 4.75 s.