RLC Power

Electricity and Magnetism Level 3

The following R L C RLC circuit is excited by an AC voltage source whose RMS magnitude is given. How much active power (in watts) is dissipated in the circuit?


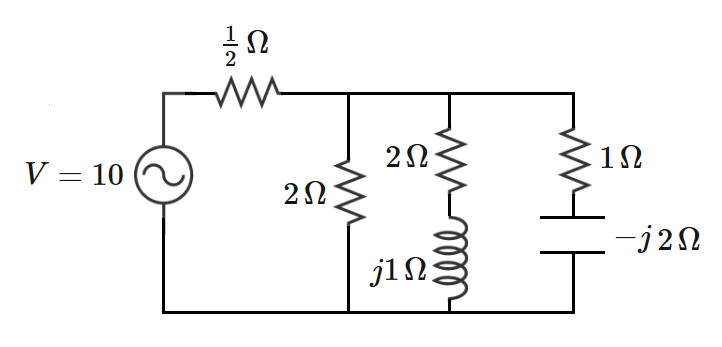
The answer is 71.503.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Max Yuen
Apr 30, 2019

I can't think of any other way other than to just add up the impedances (in ohms):

Z t o t = 1 2 + ( 1 2 + 1 2 + j + 1 1 − 2 j ) − 1 = 1 2 + ( 1 2 + 3 − j 4 − 3 j ) − 1 = 1 2 + ( 10 − 5 j 8 − 6 j ) − 1 = 1 2 + 8 − 6 j 10 − 5 j = 26 − 17 j 20 − 10 j Z_{tot} = \frac{1}{2} + \left(\frac{1}{2}+\frac{1}{2+j}+\frac{1}{1-2j}\right)^{-1}\\ =\frac{1}{2} + \left(\frac{1}{2}+\frac{3-j}{4-3j}\right)^{-1}\\ =\frac{1}{2} + \left(\frac{10-5j}{8-6j}\right)^{-1}\\ =\frac{1}{2} + \frac{8-6j}{10-5j} = \frac{26-17j}{20-10j}

Complex Power = V 2 Z t o t = 100 20 − 10 j 26 − 17 j = 100 ( 20 − 10 j ) ( 26 + 17 j ) ( 26 − 17 j ) ( 26 + 17 j ) = 100 690 + 8 j 965 \frac{V^2}{Z_{tot}}=100\frac{20-10j}{26-17j}=100\frac{(20-10j)(26+17j)}{(26-17j)(26+17j)}=100\frac{690+8j}{965}

The real part is 69000 / 965 = 71.503 69000/965=71.503

2 Helpful 2 Interesting 0 Brilliant 0 Confused

Impedance of the circuit is 1.389244398945 Ohm. Therefore power dissipated in it is 100/1.389244398945=71.503 Watts.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...