RLC Switching - Quantitative

We can use Laplace transform to solve this. After taking the transform to the circuit, we get:

• The source is $V(s)=\dfrac{10}{s}$ .
• The impedance of the resistor is $R=1$ .
• The impedance of the capacitor is $X_C=\dfrac{1}{s}$ .
• The impedance of the inductor is $X_L=s$ .

Then we have $I_R(s) = \dfrac{V(s)}{R + \dfrac{X_C X_L}{X_C + X_L}} = \dfrac{10(s^2+1)}{s(s^2+s+1)}$ .

We propose the following partial fraction descomposition: $I_R(s) = \dfrac{A}{s} + \dfrac{z}{s-z_1} + \dfrac{\overline{z}}{s-z_2}$ , where $z_{1,2}=-\dfrac{1}{2} \pm \dfrac{\sqrt{3}}{2}i$ are the roots of $s^2+s+1=0$ .

Hence we have: $A=I_R(s)(s-0) |_{s=0}=10$ and $z=I_R(s)(s-z_1) |_{s=z_1}=\dfrac{10}{\sqrt{3}}i$ .

Take inverse Laplace transform: $i_R(t) = A + ze^{z_1 t} + \overline{z}e^{z_2 t} = 10 + \dfrac{10}{\sqrt{3}}ie^{\left( -\frac{1}{2}+\frac{\sqrt{3}}{2}i \right)t} - \dfrac{10}{\sqrt{3}}ie^{\left( -\frac{1}{2}-\frac{\sqrt{3}}{2}i \right)t} = 10 - \dfrac{20}{\sqrt{3}} e^{-\frac{t}{2}} \sin\left(\dfrac{\sqrt{3}}{2}t\right)$ .

Now, $i_R'(t) = -\dfrac{20}{\sqrt{3}} e^{-\frac{t}{2}}\left( -\dfrac{1}{2}\sin\left(\dfrac{\sqrt{3}}{2}t\right) + \dfrac{\sqrt{3}}{2} \cos\left(\dfrac{\sqrt{3}}{2}t\right) \right)$ . The minimum value will occur at the first positive solution of $i_R'(t)=0$ and the maximum value at the second.

So, $i_R'(t) = 0 \implies \dfrac{1}{2}\sin\left(\dfrac{\sqrt{3}}{2}t\right) = \dfrac{\sqrt{3}}{2} \cos\left(\dfrac{\sqrt{3}}{2}t\right) \implies \tan\left(\dfrac{\sqrt{3}}{2}t\right) = \sqrt{3} \implies t = \dfrac{2}{\sqrt{3}}\left(\dfrac{\pi}{3} + \pi k\right)$ .

Finally:

• The minimum current will occur at $t_{min}=\dfrac{2\pi}{3\sqrt{3}}$ with value $i_R(t_{min})=10\left(1-e^{-\frac{\pi}{3\sqrt{3}}}\right)$ .
• The maximum current will occur at $t_{max}=\dfrac{8\pi}{3\sqrt{3}}$ with value $i_R(t_{max})=10\left(1+e^{-\frac{4\pi}{3\sqrt{3}}}\right)$ .
• The ratio is $\dfrac{i_R(t_{max})}{i_R(t_{min})}=\dfrac{1-e^{-\frac{\pi}{3\sqrt{3}}}}{1+e^{-\frac{4\pi}{3\sqrt{3}}}} \approx \boxed{2.4003}$ .

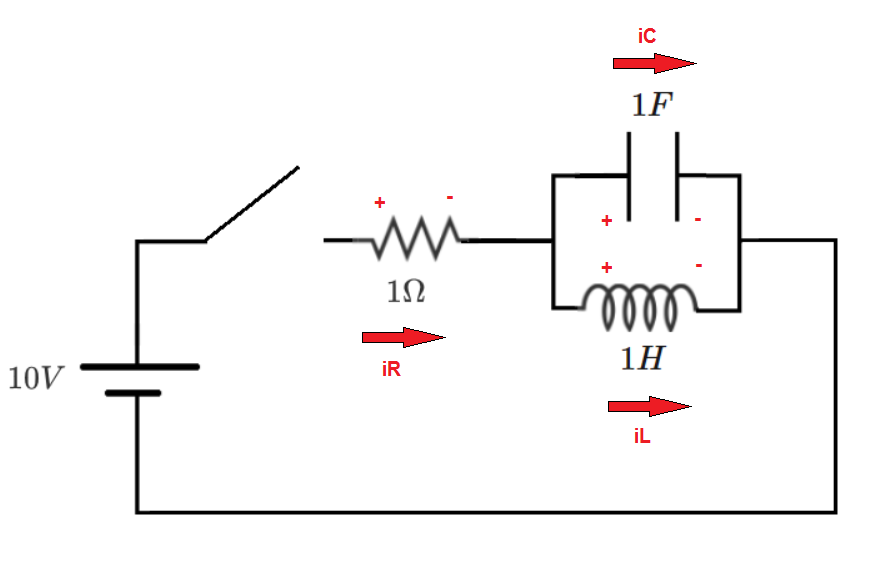
The system state variables are the capacitor voltage and the inductor current. Write expressions for the time-derivatives of the state variables in terms of the state variables and the forcing function (the DC source voltage). Note the voltage and current polarity conventions in the diagram.

Capacitor:

$\large{i_C = C \frac{dv_C}{dt} \\ i_R - i_L = C \frac{dv_C}{dt} \\ \frac{v_S - v_C}{R} - i_L = C \frac{dv_C}{dt} \\ \frac{dv_C}{dt} = \frac{\frac{v_S - v_C}{R} - i_L}{C}}$

Inductor:

$\large{v_L = L \frac{d i_L}{dt} \\ v_C = L \frac{d i_L}{dt} \\ \frac{d i_L}{dt} = \frac{v_C}{L}}$

Numerical integration yields a minimum resistor current value of 4.537, and a maximum value of 10.891, with the ratio of the two being approximately 2.4. The current reaches a constant value of 10 amps in steady-state, as expected.