RLC Transient (3-1-2020)

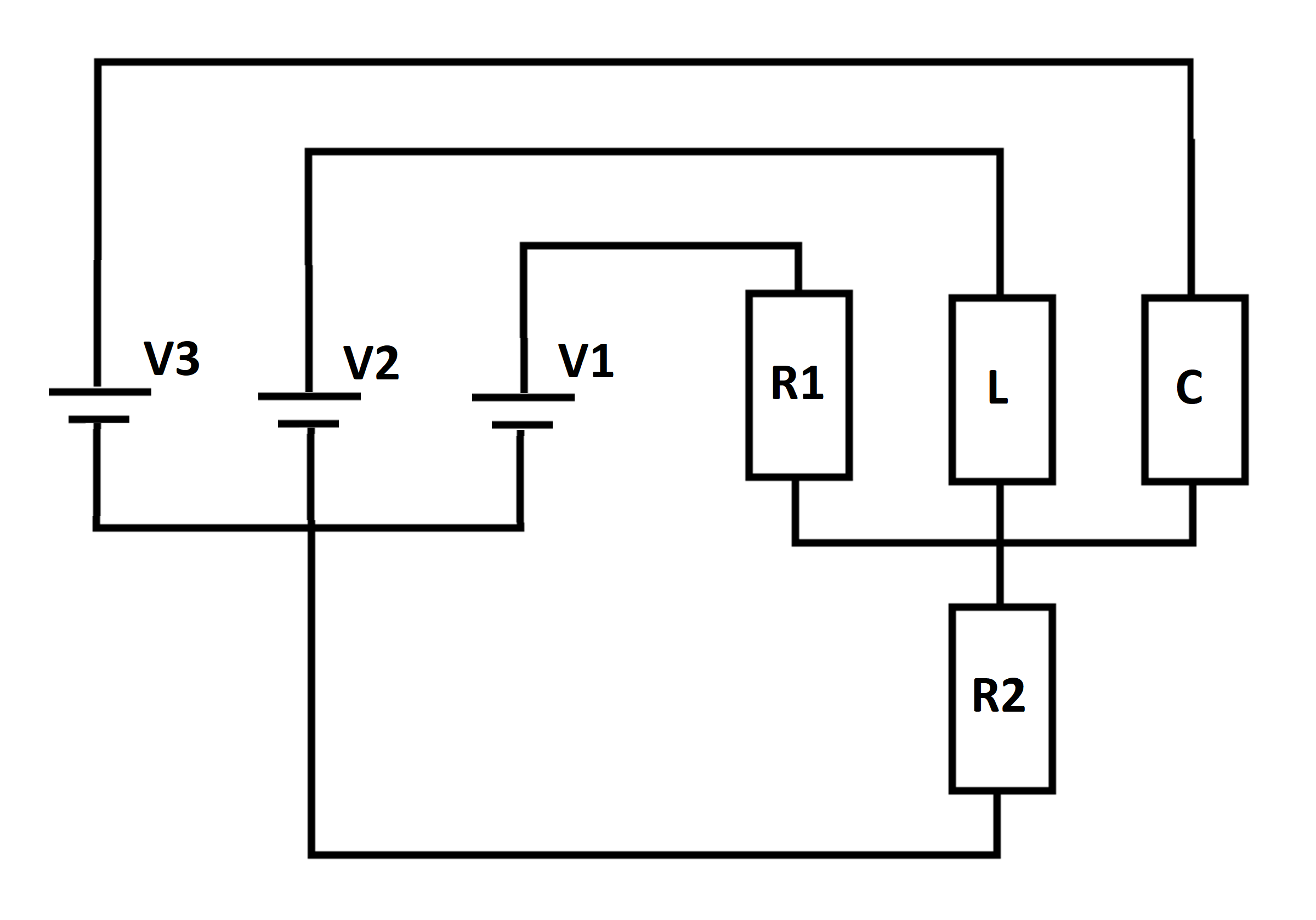
Electricity and Magnetism Level pending

Three DC voltage sources energize an RLC network, as shown below. At time $t = 0$ , the inductor and capacitor are de-energized. Let $I_0$ be the current flowing in resistor $R_2$ at time $t = 0$ . Let $I_\infty$ be the limiting value of the current flowing in resistor $R_2$ as the elapsed time approaches infinity. Let $I_{min}$ be the smallest value of current flowing in resistor $R_2$ over all time. Let $I_{max}$ be the largest value of the current flowing in $R_2$ for $t > 10$ .

Determine the following ratio:

$\large{\frac{I_{min} + I_{max}}{I_0 + I_\infty}}$

Details and Assumptions:
1) $V_1 = 10$
2) $V_2 = 20$
3) $V_3 = 30$
4) $R_1 = 1$
5) $R_2 = 2$
6) $L = 1$
7) $C = 5$
8) All four currents are positive numbers

The answer is 0.693.

1 solution

Steven Chase
Mar 1, 2020

The state variables are the inductor $I_L$ current and the capacitor voltage $I_C$ . Let the voltage across $R_2$ be $V_{R2}$ . The state-space model is:

$V_{R2} = V_3 - V_C \\ I_{R1} = \frac{V_1 - V_{R2}}{R_1} \\ I_{R2} = \frac{V_{R2}}{R2} \\ V_L = V_2 - V_{R2} = L \dot{I}_L \\ I_C = I_{R2} - I_{R1} - I_L = C \dot{V}_C$

Numerical integration results in the following plot of $I_{R2}$ . At time $t = 0$ , the capacitor voltage is zero, meaning that $V_3$ appears across $R_2$ , resulting in $\frac{30}{2} = 15$ units of current. At $t = \infty$ , the inductor is a short circuit, meaning that $V_2$ appears across $R_2$ , resulting in $\frac{20}{2} = 10$ units of current. Since the circuit has both capacitance and inductance, there is an intermediate transient with damped oscillation.

@Steven Chase wow nice question I can't able to solve but i can understand the solution. Please post more question like this. I want to solve more questions like this .

A Former Brilliant Member - 1 year, 3 months ago

RLC Transient (3-1-2020)

The answer is 0.693.

1 solution

0 pending reports