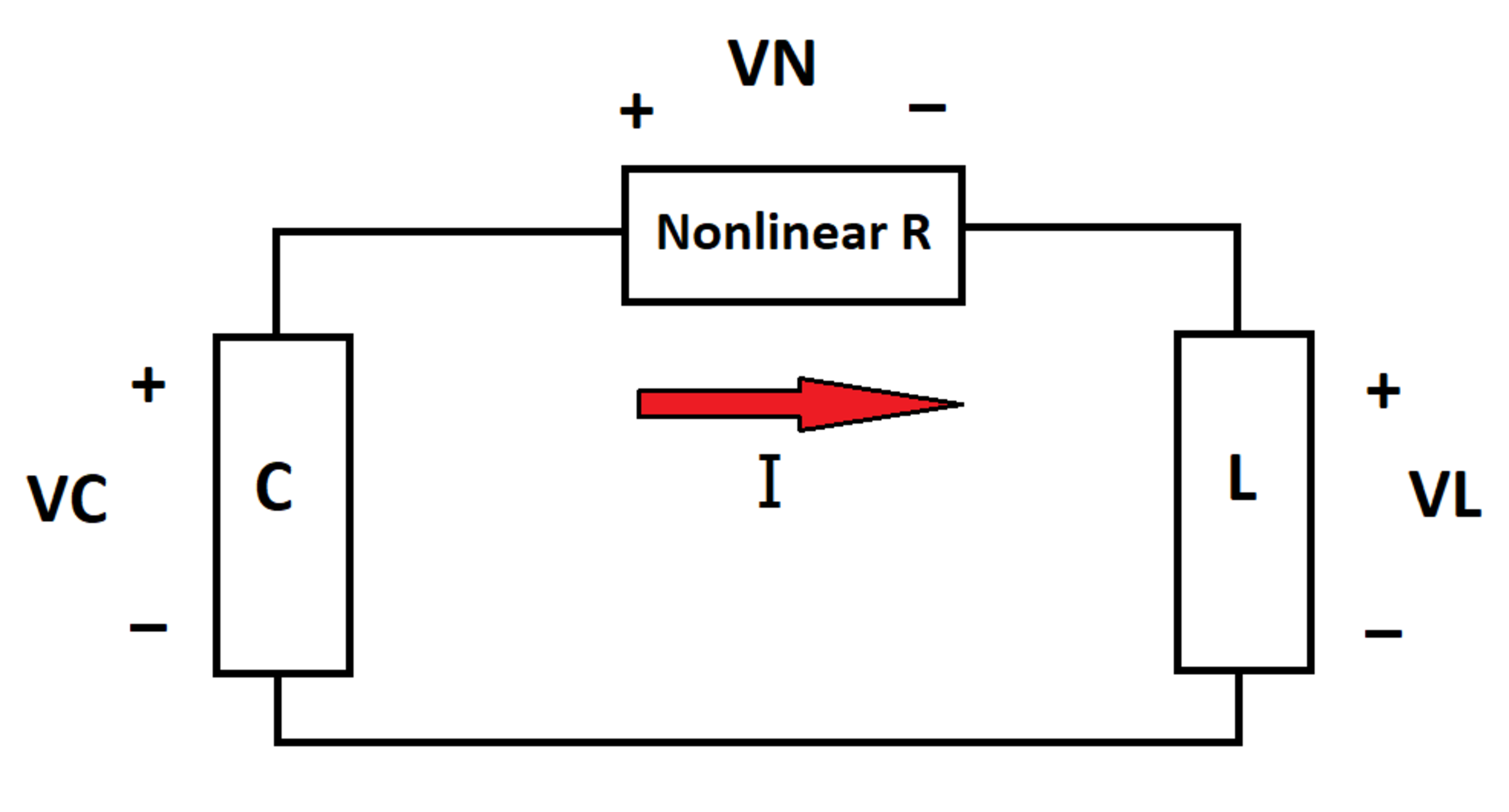
RLC with Nonlinear Resistor

The circuit equations are:

$-\frac{Q}{C} + V_N + L\dot{I} = 0$ $-\dot{Q}=I$ $\dot{V}_N = R_o \mathrm{e}^{-\alpha V_N} \dot{I}$ $V_N(0)=I(0)=0 \ ; \ Q(0) = 10$

$Q$ is the instantaneous charge on the capacitor and $I$ is the current flowing in the circuit. Now, numerical integration does the rest. A plot for the cases $\alpha = 1$ and $\alpha = 0$ are shown below. For the case $\alpha=0$ , one can see that $V_N$ is twice the value of $I$ at all instants of time. This is the linear behaviour of Ohm's law. For the case $\alpha=1$ , this is clearly not the case. Moreover, when $\alpha=1$ , the capacitor discharges to a point of opposite electric polarity and then again discharges from that instant to zero.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

clear all, clc

% Circuit parameters:
Ro   = 2; alpha   = 1; L   = 1; C   = 1;

% Time and time-step initialisation:
tf   = 10; dt     = 1e-6; t   = 0:dt:tf;

% Initial Conditions:
I(1) = 0; VN(1)   = 0; Q(1)   = C*10;

for k = 1:length(t)-1

    % Governing differential equations:
    dI       = (Q(k)/C - VN(k))/L;
    dQ       = -I(k);
    dVN      = Ro*exp(-alpha*VN(k))*dI;

    % Explicit Euler numerical integration:
    I(k+1)   = I(k) + dt*dI;
    Q(k+1)   = Q(k) + dt*dQ;
    VN(k+1)  = VN(k) + dt*dVN;
end

ANSWER   = VN(end)*I(end)               % ANSWER = 0.7683

With the initial conditions $V_N=0$ at $I=0$ we solve the differential equation for the non-linear resistor: $\begin{aligned} R_0 &= V_N^{(1)} (I) e^{\alpha V_N(I)} = \frac{1}{\alpha}\cdot\frac{d}{dI} e^{\alpha V_N(I)} &&& \Rightarrow &&&& R_0 (I - 0) &= \frac{1}{\alpha}\left[ e^{\alpha V_N(I)} - e^0 \right] &&&& \left| \begin{gathered} I\rightarrow I'\\ \int_0^I\ldots dI' \end{gathered} \right. \end{aligned}$ We solve for $I$ to notice the non-linear resistor is in fact a diode, because it has the equation of a diode: $\begin{aligned} I&=\frac{1}{\alpha R_0}\left(e^{\alpha V_N(I)} - 1\right) &&&\Rightarrow &&&& V_N(I) &=\frac{1}{\alpha}\log (\alpha R_0 I + 1)=\log(2I+1) \end{aligned}$ Let the state vector be $\vec{x}(t)=(V_C,\: I)^T(t)$ . Then we can use KCL for the first equation and KVL for the second equation of the state space system: $\begin{aligned} \begin{pmatrix} C V_C^{(1)}(t)\\[.5em] L I^{(1)}(t) \end{pmatrix} &=\begin{pmatrix} -I(t)\\[.5em]V_C(t) - V_N(I) \end{pmatrix} &&&\underset{C=L=1}{\Rightarrow} &&&&\vec{x}^{(1)}(t) &= \begin{pmatrix} -I(t)\\[.5em]V_C(t) - \log(2I(t) + 1) \end{pmatrix} =: \vec{f}(\vec{x}(t)), &&&\vec{x}(0) &= \begin{pmatrix}10\\0\end{pmatrix} \end{aligned}$ We have to solve this non-linear system of equation numerically (see below) and get $P(10)\approx \boxed{0.768}$ .

/* maxima program to find P(10) */
/* define state space system */
ode : [
    -i,                 /* = d/dt vc(t) */
    vc - log(2 * i + 1) /* = d/dt i(t) */
]$

/* solve ode numerically via 4th order runge-kutta */
result : rk(ode,
    [vc, i],            /* state vector */
    [10, 0],            /* initial conditions */
    ['t, 0, 10, 1e-2]   /* t in [0; 10] with step-size 1e-2 */
)$

/* calculate power VN * I at t = 10 (result colums: [t, vc, i]) */
P : log(2 * last(result)[3] + 1) * last(result)[3];

Rem.: Let's take a look at $V_C(t)$ and $I(t)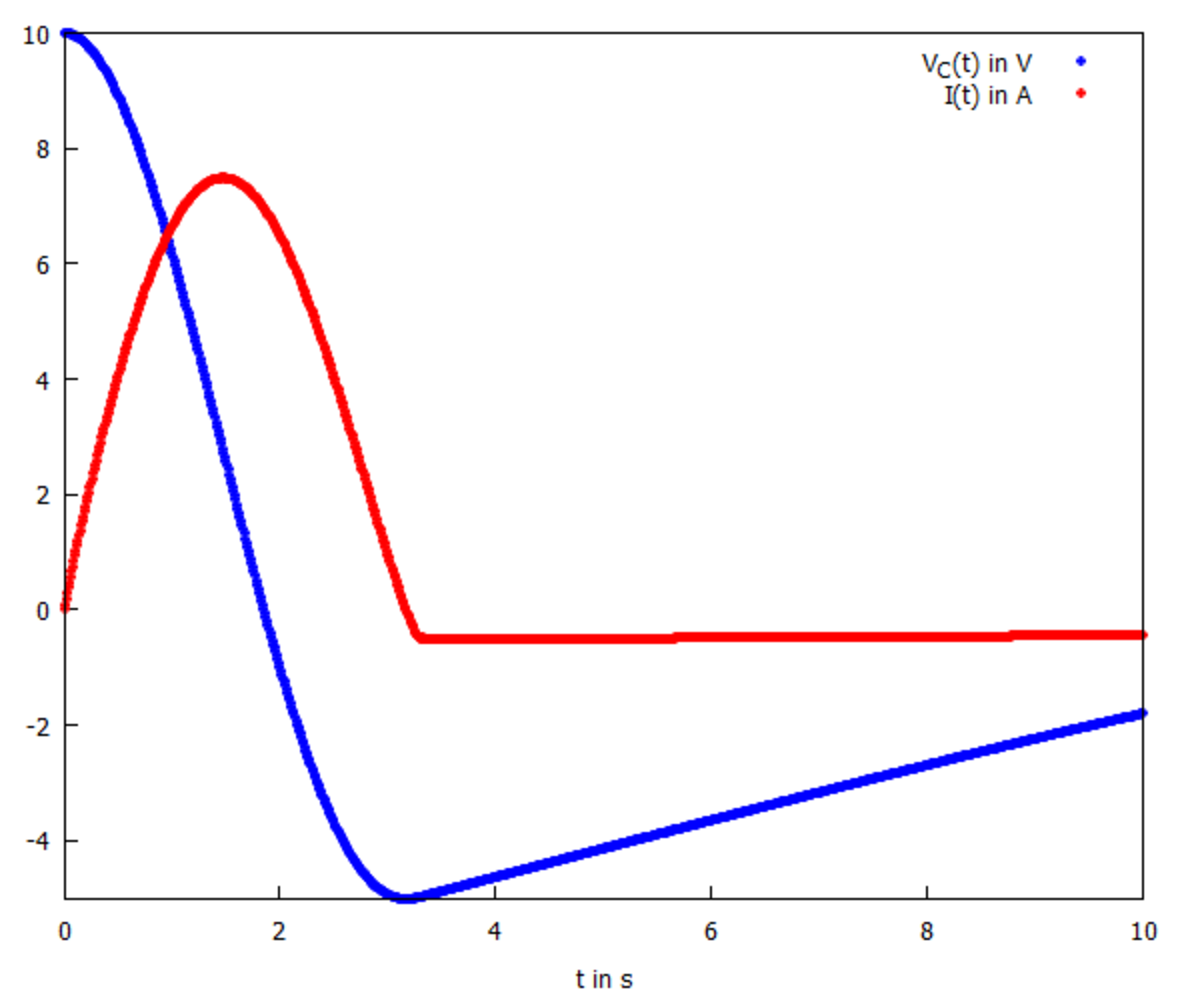$ : Let's try to make sense of what we see: For $0\leq t\leq 3.1$ , the current is positive, so the diode let's the current through and acts similar to a small resistor. As a result, both current and voltage look similar to the cosine and sine we would expect of the ideal LC-circuit without the diode.

For $t>3.1$ , the current changes its sign and the diode starts blocking the current: It acts similar to a large resistor! As a result, the voltage looks like a slowly decaying exponential - exactly what we would expect of a series RCL-circuit with a large resistor! The same is true for the current, but it is too small to see in the graph above.