RLC Y Circuit (Part 2)

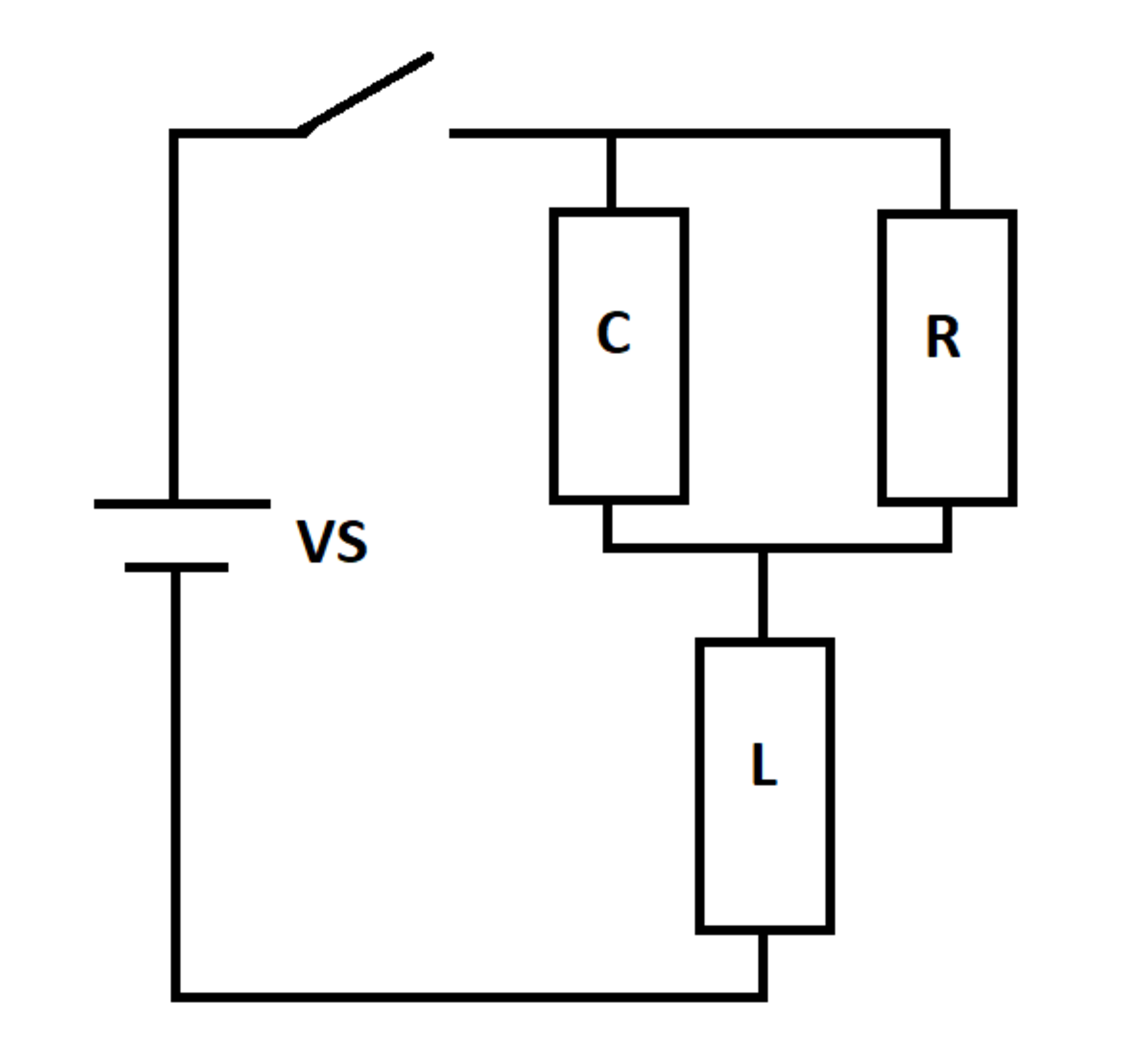
Electricity and Magnetism Level pending

An RLC circuit is excited by a DC voltage source. The switch closes at time $t = 0$ , at which time the inductor and capacitor are de-energized.

Let $I_{min}$ and $I_{max}$ be the smallest and largest source current values for $t > 2$ . Let $I_{0+}$ be the source current right after the switch closes, and let $I_{\infty}$ be the steady-state source current as the elapsed time approaches infinity.

Determine the following ratio:

$\large{\frac{I_{min} + I_{max}}{I_{0+} + I_{\infty}}}$

Details and Assumptions:
1) There are no negative numbers in the ratio
2) $R = L = C = 1$
3) $V_S = 10$
4) The circuit topology has changed relative to the previous problem

The answer is 2.2498.

1 solution

Karan Chatrath
Dec 1, 2019

The circuit equations based on Kirchoff's laws are as follows. $I_R$ is the current through the resistor, $I_C$ is that through the capacitor and $I_L$ is that through the inductor. The charge on the capacitor is $Q$ .

$I_RR + L\frac{dI_L}{dt} = V_S$ $I_RR = \frac{Q}{C}$ $I_L = I_R + I_C$ $I_C = \frac{dQ}{dt}$

At $t = 0$ the charge on the capacitor and all currents are zero.

By manipulating the above equations, we get:

$\frac{dI_R}{dt} + \frac{dI_R}{dt} = -I_R + V_S$ $\frac{dI_R}{dt} = I_C$

Now this can be rearranged as:

$\left[\begin{matrix}1&1\\1&0\end{matrix}\right]\left[\begin{matrix}\dot{I}_R\\\dot{I}_C\end{matrix}\right] = \left[\begin{matrix}-1&0\\0&1\end{matrix}\right]\left[\begin{matrix}I_R\\I_C\end{matrix}\right] + \left[\begin{matrix}1\\0\end{matrix}\right]V_S$

Which implies:

$\left[\begin{matrix}\dot{I}_R\\\dot{I}_C\end{matrix}\right] =\left[\begin{matrix}1&1\\1&0\end{matrix}\right]^{-1}\left[\begin{matrix}-1&0\\0&1\end{matrix}\right]\left[\begin{matrix}I_R\\I_C\end{matrix}\right] + \left[\begin{matrix}1&1\\1&0\end{matrix}\right]^{-1} \left[\begin{matrix}1\\0\end{matrix}\right]V_S$

Also:

$I_L = \left[\begin{matrix}1&1\end{matrix}\right]\left[\begin{matrix}I_R\\I_C\end{matrix}\right]$

Using shorthand notation:

$\boxed{\dot{x} = Ax + Bu \ ; \ I_L = Cx}$ Where: $A = \left[\begin{matrix}1&1\\1&0\end{matrix}\right]^{-1}\left[\begin{matrix}-1&0\\0&1\end{matrix}\right]$ $B = \left[\begin{matrix}1&1\\1&0\end{matrix}\right]^{-1} \left[\begin{matrix}1\\0\end{matrix}\right]$ $C = \left[\begin{matrix}1&1\end{matrix}\right]$ $x = \left[\begin{matrix}I_R\\I_C\end{matrix}\right]$

Now, numerical integration does the rest. This can also be solved analytically. A plot of $I_L$ vs. Time is:

From here, the required answer is computed which comes out to be approximately $\boxed{2.25}$ .

Nice problem. I suggest a third version of this problem with the resistor and inductor in parallel, in combination with the capacitor in series, would complete this 'Y-circuit' problem set.

Karan Chatrath - 1 year, 6 months ago

Thanks for the solution. I will post "Part 3" as well. I find these little circuit transient problems to be rather addictive

Steven Chase - 1 year, 6 months ago

I enjoy these problems too. Thanks for sharing. It would be fun to analyze these circuits in the frequency domain. But I think that's already covered in the domain of AC circuits.

Karan Chatrath - 1 year, 6 months ago

RLC Y Circuit (Part 2)

The answer is 2.2498.

1 solution

0 pending reports