RLC Y Circuit (Part 3)

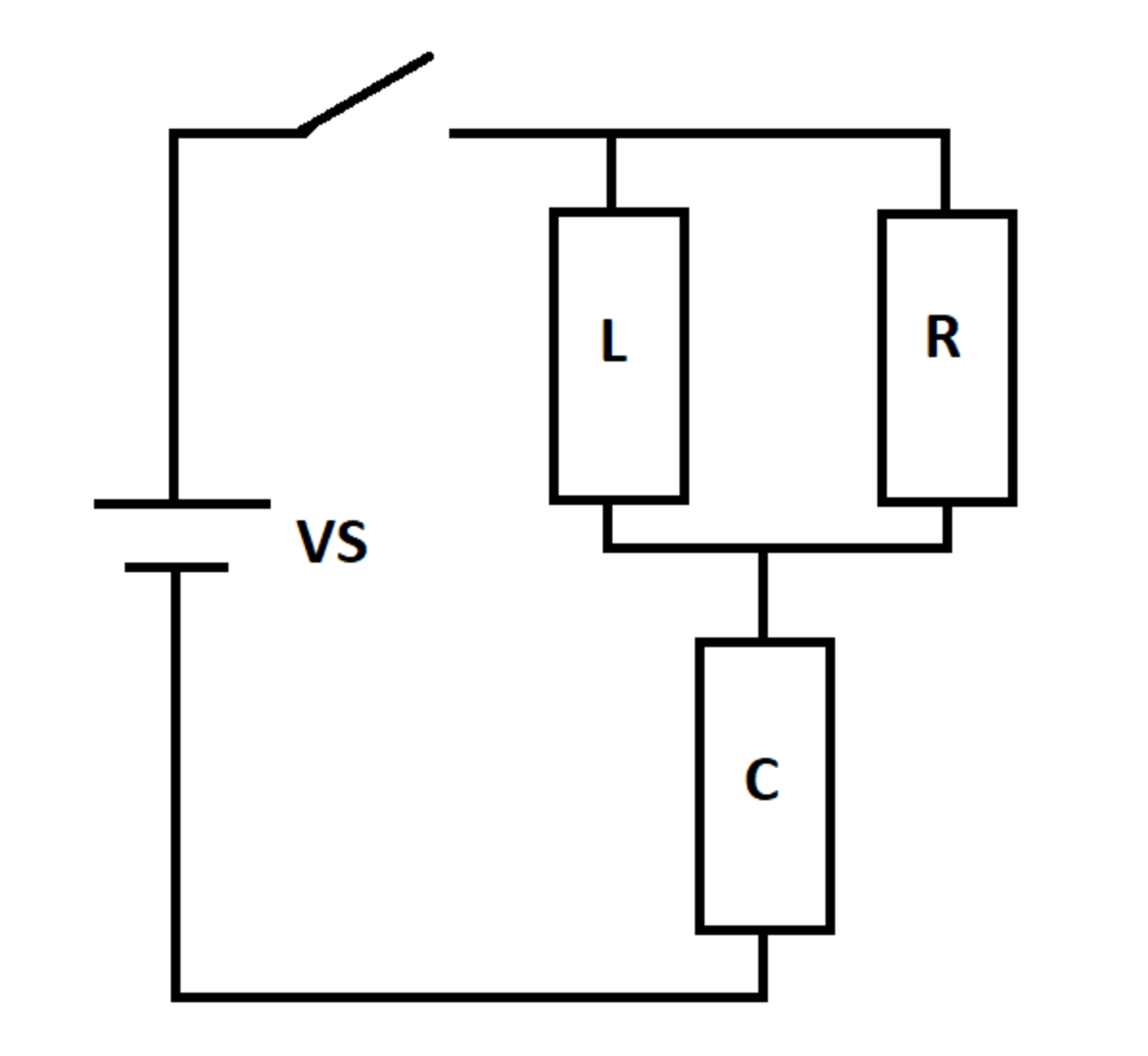
Electricity and Magnetism Level pending

An RLC circuit is excited by a DC voltage source. The switch closes at time $t = 0$ , at which time the inductor and capacitor are de-energized.

Let $I_{min}$ and $I_{max}$ be the smallest and largest source current values for $t > 3$ (note that sign matters). Let $I_{0+}$ be the source current right after the switch closes, and let $I_{\infty}$ be the steady-state source current as the elapsed time approaches infinity.

Determine the following ratio:

$\large{\frac{I_{min} + I_{max}}{I_{0+} + I_{\infty}}}$

Details and Assumptions:
1) $I_{min}$ is the only negative number of the four
2) $R = L = C = 1$
3) $V_S = 10$

The answer is -0.1365.

1 solution

Karan Chatrath
Dec 1, 2019

Let the current through the resistor be $I_R$ , through the inductor be $I_L$ and that through the capacitor be $I_C$ . The charge on the capacitor is $Q$ .

Then using Kirchoff's laws:

$\red{V_S = I_RR +\frac{Q}{C}} \ ; \ \blue{I_RR = L\frac{dI_L}{dt}} \ ; \ \green{I_C = I_R + I_L} \ ; \ \orange{I_C = \frac{dQ}{dt}}$

By inspecting the circuit, one can conclude that $I_R(0) = 10$ and $I_L(0) = 0$ .

By manipulating the above equations and rearranging:

$\left[\begin{matrix}\dot{I}_L\\\dot{I}_R\end{matrix}\right] = \left[\begin{matrix}0&1\\-1&-1\end{matrix}\right]\left[\begin{matrix}I_L\\I_R\end{matrix}\right] \ ; \ I_C = \left[\begin{matrix}1&1\end{matrix}\right]\left[\begin{matrix}I_L\\I_R\end{matrix}\right]$

Having obtained this state-space form, it can be written in a short hand notation and numerically integrated to obtain the following solution:

The required answer of $\boxed{-0.1365}$ follows naturally from here.

RLC Y Circuit (Part 3)

The answer is -0.1365.

1 solution

0 pending reports