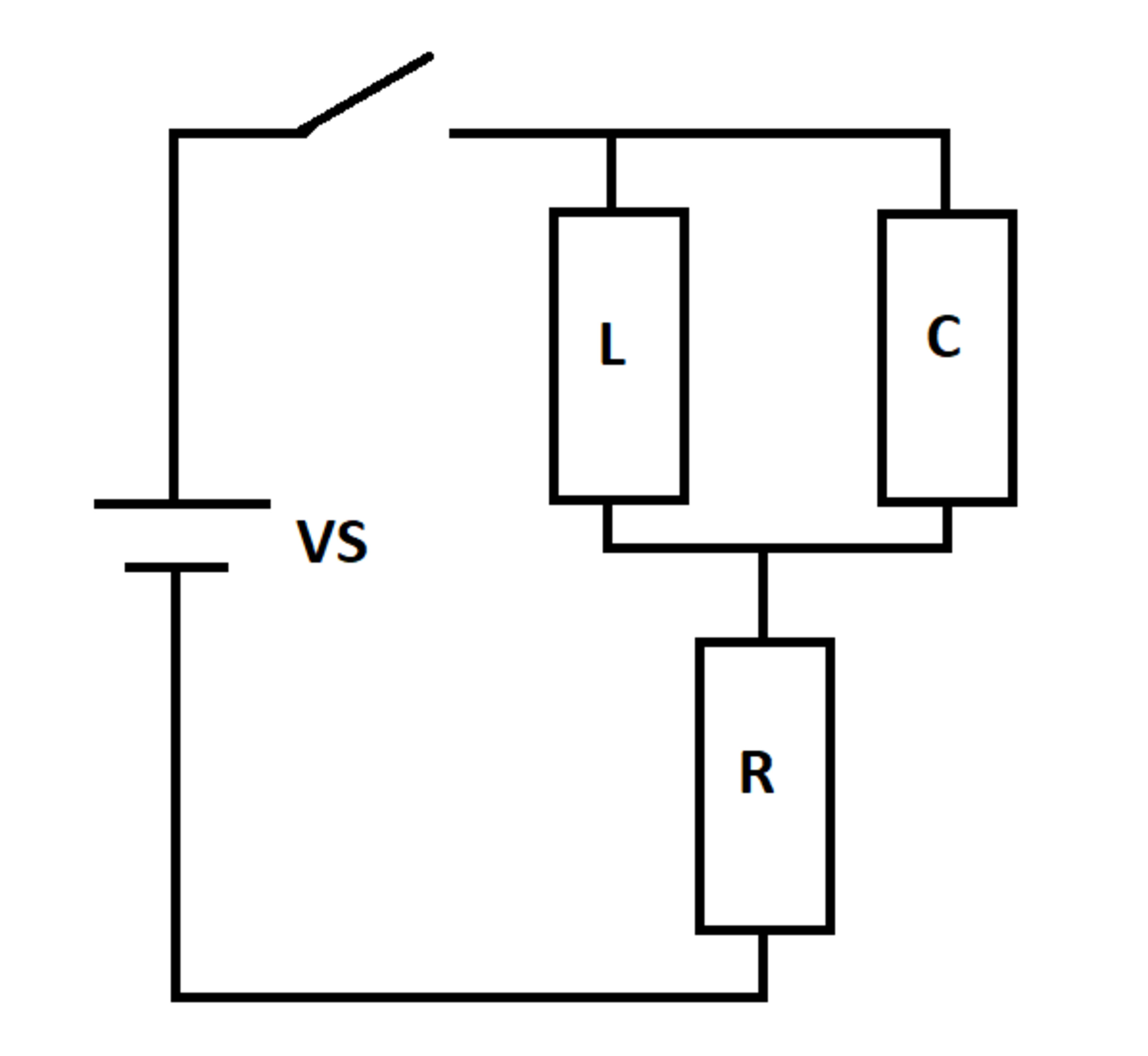
RLC Y Circuit

My approach is essentially the same as the one presented by @Karan Chatrath, but with some logistical/stylistic differences. The state variables are the capacitor voltage $V_C$ and the inductor current $I_L$ .

Since the capacitor and inductor are in parallel, we have the first state-space equation:

$V_C = L \dot{I}_L \\ \dot{I}_L = \frac{V_C}{L}$

Then using Kirchoff's Voltage Law:

$V_S - V_C - R (I_L + I_C) = 0 \\ V_S - V_C - R (I_L + C \dot{V}_C) = 0 \\ \dot{V}_C = \frac{V_S - V_C}{R C} - \frac{I_L}{C}$

Numerical integration takes care of the rest, now that we have the rates of change of the state variables expressed in terms of the state variables and the forcing function. And finally,

$I_S = I_L + I_C = I_L + C \dot{V}_C$

The plot of source current vs. time is below. Simulation code is attached as well.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

import math

VS = 10.0

R = 1.0
L = 1.0
C = 1.0

##################################

dt = 10.0**(-5.0)
t = 0.0
count = 0

IL = 0.0
VC = 0.0

ILd = 0.0
VCd = 0.0

ISmax = -999999999.0
ISmin = 99999999.0

while t <= 30.0:

    IL = IL + ILd * dt
    VC = VC + VCd * dt

    ILd = VC/L

    VCd = (VS-VC)/(R*C) - IL/C

    IC = C*VCd

    IS = IL + IC

    if IS > ISmax:
        ISmax = IS
    if IS < ISmin:
        ISmin = IS

    t = t + dt
    count = count + 1

    #if count % 1000 == 0:
        #print t,IS,IL,VC

##################################

print dt
print ""
print ISmin
print ISmax
print ""
print ((ISmin+ISmax)/20.0)

A general outline of the solution. I have omitted specifics.

Applying Kirchoff's laws to the circuit gives the following relations. Note that current through the inductor is $I_L$ and that through the capacitor is $I_C$ and the charge stored in the capacitor is $Q$ . The source current is denoted by $I$ .

$-V_S + L\frac{dI_L}{dt} +IR = 0$ $L\frac{dI_L}{dt} - \frac{Q}{C} = 0$ $\frac{dQ}{dt} = I_C$ $I = I_L+I_C$

By some straightforward manipulation, it can be shown that:

$\frac{d^2I_L}{dt} +\frac{dI_L}{dt} + I_L = 10 \ ; \ \frac{d^2I_L}{dt} = I_C$

Initial conditions are:

$I_L(0) = 0 \ ; \ Q(0) = 0 \implies \dot{I}_L(0) = 0$

The closed-form solution of $I_L(t)$ needs to be double differentiated to get the capacitor current. Finally, the expression for source current can be obtained. It can be verified by inspecting the circuit that the source current $I$ as soon as the switch closes and after a large amount of time is both $10A$ . By searching (either using a computer program or by using differential calculus) for the max and min current and computing the required ratio, the answer is $\boxed{0.7714}$ .