This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Moderator note:
Simple standard approach.
Nice use of AM-GM! Good work.
You should ask for the maximum value of a b c in the question.
well done :)
Why only restrict to natural numbers? It is true for all positive real numbers. Also , a , b , c need not be distinct. Infact the equality occurs ⟺ a = b = c = 1 .
i didn't understand what you did :/
Log in to reply
Check up Applying the Arithmetic Mean Geometric Mean Inequality
Standard solution by Cauchy Schwarz:
( 1 + a ) ( 1 + b ) ( 1 + c ) 8 1 + 3 a b c 3 a b c a b c ≥ ( 1 + 3 a b c ) 3 ≥ ( 1 + 3 a b c ) 3 ≤ 2 ≤ 1 ≤ 1
Therefore, the maximum value of a b c = 1 .
Can you please explain how the chauchy schwartz is applied? I cant understand....
As gernally8=2 2 2so a+1=2 a=1. Similarly b=1=a=c
You only proved equality
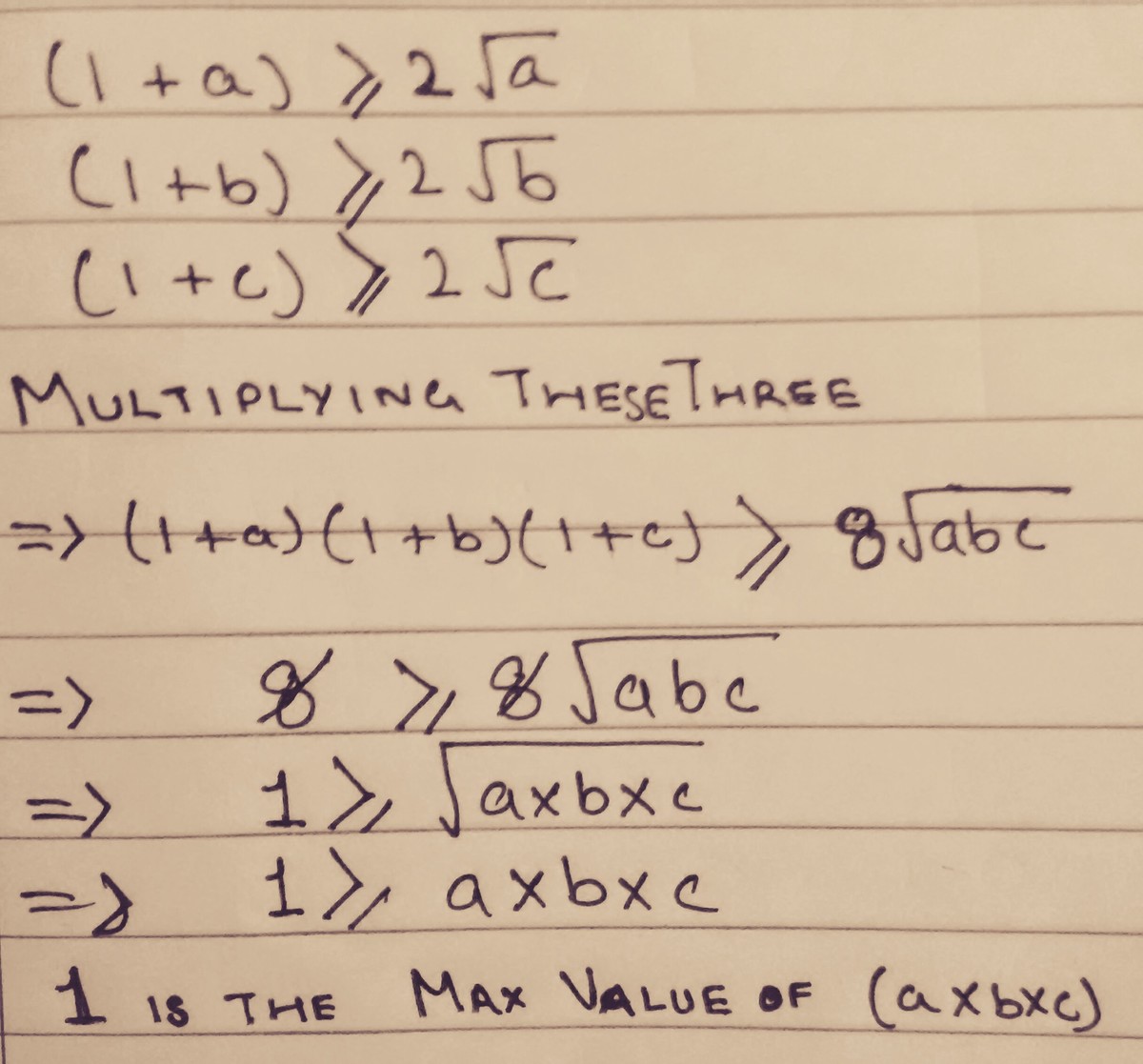
By applying A M − G M on ( 1 , a ) , ( 1 , b ) and ( 1 , c ) : 2 1 + a ≥ a ; 2 1 + b ≥ b ; 2 1 + c ≥ c
Therefore, 2 × 2 × 2 ( 1 + a ) ( 1 + b ) ( 1 + c ) ≥ a b c ( 1 + a ) ( 1 + b ) ( 1 + c ) ≥ 8 a b c ⟹ 1 ≥ a b c a b c ≤ 1