RMS Current With Harmonics
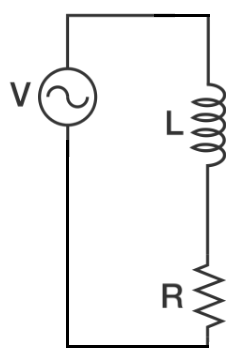
An ideal AC voltage source is connected in series with a 1 Ω resistance and a 1 H inductance. The source voltage (in volts) is given by:
V ( t ) = 2 cos ( t ) + 2 cos ( 2 t )
What is the RMS (root-mean-square) value of the current flowing in the circuit (in amps, to 3 decimal places)?
Note: Assume the period of the composite signal to be the fundamental period.
The answer is 0.837.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I think this method is not a general method specifically the Euclidean Norm.
Consider a situation in which the two signals are of same frequency and using the superposition method we get the two currents as I 1 = I 2 = 2 cos t . Thus, the total current I = 2 2 cos t and I rms = 2 .
Now, let us use the Euclidean Norm, I 1 rms = I 2 rms = 1
I rms = I 1 rms 2 + I 2 rms 2 = 2
Hence, from both the methods the answers are not matching.
I agree that in this particular problem this method will work.
Log in to reply
Yes, I forgot to mention that you have to consolidate like-frequency terms before applying it. The Euclidean norm only applies to terms with distinct frequencies.
There are two ways to do this problem. The hard way is determining the time-domain representation of the signal and then integrating to get the RMS value. The easy way is to use Superposition and apply Parseval's Theorem . This sounds more complicated than it actually is.
We have two frequencies in the source; one signal with an RMS value V 1 = 1 and angular frequency ω 1 = 1 , and the other with an RMS value V 2 = 1 and angular frequency ω 2 = 2 . We can represent the circuit as a superposition of two circuits: one at each frequency.
The complex reactance of an inductor is X L = ω L . Since L = 1 , X L = ω . The key is that at each frequency, the resistance remains constant (at least ideally) while the inductive reactance scales with frequency.
Circuit 1: ω = 1 ; R = 1 ; X L = 1 ; Z = R + j X L = 1 + j ; ∣ Z ∣ = 1 2 + 1 2 = 2
Circuit 2: ω = 2 ; R = 1 ; X L = 2 ; Z = R + j X L = 1 + 2 j ; ∣ Z ∣ = 1 2 + 2 2 = 5
Then we can calculate the RMS current magnitudes in both circuits using Ohm's Law .
I 1 = 2 1 I 2 = 5 1
Finally, in this application, Parseval's Theorem tells us that the RMS value of the composite current is the square root of the sum of the squares of the RMS currents at each frequency (the Euclidean Norm).
I R M S = I 1 2 + I 2 2 = 2 1 + 5 1 = 1 0 7 ≈ 0 . 8 3 7
As one final note, I also did it the semi-hard way by running a small-time-step simulation in code and numerically integrating. That approach gives the same result as the method presented above.