Robo Space Valley

Classical Mechanics Level 4

Robo space volley

A volleyball can be molded as a non stretchable but flexible spherical envelop of mass m =4kg and radius R =5metre filled with air at excess pressure P.The excess pressure remains unchanged with small deformations in the volleyball when hit or when it strikes some rigid surface. Mass of the air inside the volleyball can be neglected. Such a volley ball strikes a rigid wall and bounces back without loosing speed.The whole game is played in outer space at 0 gravity

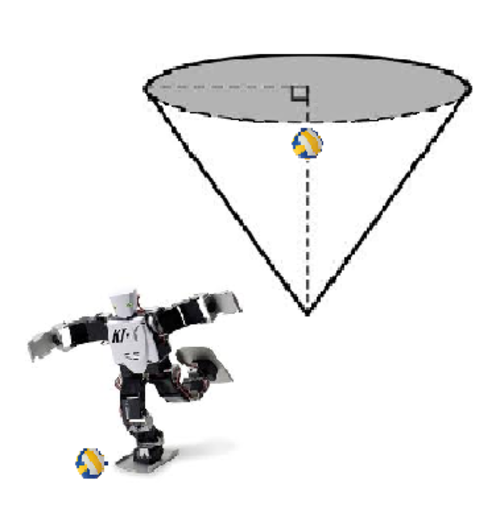
Robo -space-volley a game probably played by robos at outer space in another fifty years and will consist of flying robos at some level of height above a cone.The robos strike the ball with a kick toward the inner curved surface of the fixed conical surface. the robos can calculate time after which the ball comes again (excluding collision time ) and play a move accordingly. The only thing they cannot calculate is the time of collision. The game is to kick a volleyball towards a conical surface and then the next opponent player kicks it back and so on the one who misses loses.If the ball is initially on the the axis d distance away from the cone, the time error the other opponent robot doesn't calculate is t=2T when the first robo strikes at 15 degrees with the axis. And the angle with the axis at which the first robot should strike the ball to deceive the opponent the most is A

find A and T

The opponent can only make a move when there is no more collisions of the ball with the curved surface possible.All collisions are perfectly elastic

Details and assumptions: The semi vertical angle of the cone is 12.5 degrees. P = π 10 S I u n i t s P=\frac{\pi}{10}SI units The robots can move inside the cone and make moves accordingly. The cone can be considered of infinite curved surface.

T=7/2 s, A ϵ ( 0 o , 17. 5 o ) A\epsilon(0^{o},17.5^{o}) T=7/2 s, A = 15 d e g r e e s A=15 degrees T=7 s , A ϵ ( 0 o , 17. 5 o ] A\epsilon(0^{o},17.5^{o}] T=14 s , A ϵ ( 0 o , 1 5 o ] A\epsilon(0^{o},15^{o}]

Milun Moghe by Milun Moghe , 25, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Milun Moghe
Mar 21, 2014

Image Image

To find the total number of collisions it can be clearly seen that when the straight line PABC becomes parallel or makes a more obtuse angle with the the axis then there will be no more intersections. The number of intersections is the number of collisions . It can be given by n = [ 36 0 o − 2 ( ∠ A P O ) + ( ∠ A O P ) 2 ( ∠ A O P ) ] n=\left[\frac{360^{o}-2(\angle APO)+(\angle AOP)}{2(\angle AOP)}\right] where [.] represents GIF

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...