Rocket science
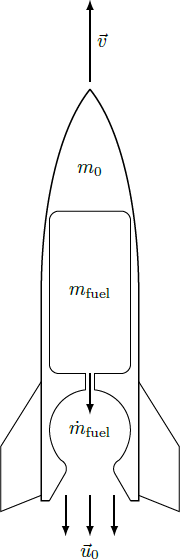
A single-stage rocket is launched vertically from the North Pole and reaches just the required escape velocity to leave the earth after burning its entire fuel.
What is the fuel mass of the rocket in units of the empty weight (rocket without fuel)?
Assumptions:
- The fuel is consumed with a constant rate and the combustion gases are expelled with a velocity from the nozzle.
- The gravitational acceleration at the North Pole is and the radial distance to the center of the earth is .
Hint: Without external forces, the total momentum of the rocket and the fuel gases must be conserved. The rocket itself changes its momentum because of its acceleration , the mass decrease , and the momentum of the ejected gas.
Bonus question: How much fuel would be saved if the rocket were started instead of the North Pole from the equator?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The momentum balance for the force-free rocket reads d t d p ⇒ v ˙ = ( d t d p ) rocket + ( d t d p ) gas = ( m ˙ v + m v ˙ ) − m ˙ ( v − u 0 ) = m ˙ u 0 + m v ˙ = ! 0 = − u 0 m m ˙ = u 0 m 0 − ∣ m ˙ ∣ ( t − t 0 ) ∣ m ˙ ∣ with the burning time t 0 = m fuel / ∣ m ˙ ∣ of the rocket. Integration from t = 0 to t 0 results the final velocity v 0 = u 0 ∫ 0 t 0 m 0 / ∣ m ˙ ∣ + t 0 − t d t = u 0 ln m 0 / ∣ m ˙ ∣ m 0 / ∣ m ˙ ∣ + t 0 = u 0 ln m 0 m 0 + m fuel The work integral over the gravitational force results the necessary energy to leave the earth: ⇒ ⇒ W v 0 m fuel = − ∫ R ∞ F d r = ∫ R ∞ G r 2 M m 0 d r = ∫ R ∞ m 0 g r 2 R 2 d r = m 0 g R = ! 2 1 m 0 v 0 2 = 2 g R = 1 1 . 1 6 7 s km = m 0 ( exp ( u 0 v 0 ) − 1 ) ≈ 4 0 . 3 7 ⋅ m 0