Rocket Science on Barges
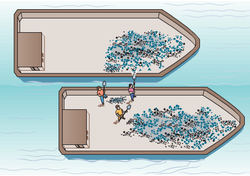 Two long barges are moving in the same direction in still water, one with a speed of 10 km/h and the other with a speed of 20 km/h. While they are passing each other, coal is
shoveled from the slower to the faster one at a rate of 1000 kg/min.
Two long barges are moving in the same direction in still water, one with a speed of 10 km/h and the other with a speed of 20 km/h. While they are passing each other, coal is
shoveled from the slower to the faster one at a rate of 1000 kg/min.
How much additional force must be provided by the driving engines of (a) the faster barge and (b) the slower barge if neither is to change speed?
Assume that the shoveling is always perfectly sideways and that the frictional forces between the barges and the water do not depend on the masses of the barges. Choose the answer that equals the sum of answers to (a) and (b).
Problem credit: Fundamentals of Physics Extended, 9th Edition
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The coal is being soveled the other way around: From the slow to the fast barge.
Nonetheless your solution is correct, I am just pointing that out.
This problem deals with the concept of VARIABLE MASS:
In the systems we have dealt with so far, we have assumed that the total mass of the system remains constant. Sometimes, as in a rocket, it does not. Most of the mass of a rocket on its launching pad is fuel, all of which will eventually be burned and ejected from the nozzle of the rocket engine.
We handle the variation of the mass of the rocket as the rocket accelerates by applying Newton’s second law, not to the rocket alone but to the rocket and its ejected combustion products taken together. The mass of this system does not change as the rocket accelerates.
Finding the Acceleration
Assume that we are at rest relative to an inertial reference frame, watching a rocket accelerate through deep space with no gravitational or atmospheric drag forces acting on it. For this one-dimensional motion, let M be the mass of the rocket and v its velocity at an arbitrary time t .

Figure 9-22b shows how things stand a time interval d t later.The rocket now has velocity v + d v and mass M + d M ,where the change in mass dM is a negative quantity. The exhaust products released by the rocket during interval dt have mass − d M and velocity U relative to our inertial reference frame. Our system consists of the rocket and the exhaust products released during interval d t .The system is closed and isolated, so the linear momentum of the system must be conserved during d t ;that is,
P i = P f , . . . . ( 9 − 8 2 )
where the subscripts i and f indicate the values at the beginning and end of time interval d t . We can rewrite Eq.9-82 as
M v = − d M ( U ) + ( M + d M ) ( v + d v ) , . . . . ( 9 − 8 3 )
where the first term on the right is the linear momentum of the exhaust products released during interval d t and the second term is the linear momentum of the rocket at the end of interval d t .
We can simplify Eq.9-83 by using the relative speed v r e l between the rocket and the exhaust products,which is related to the velocities relative to the frame with

In symbols, this means
( v + d v ) = v r e l + U
U = v + d v − v r e l . . . . ( 9 − 8 4 )
Substituting this result for U into Eq.9-83 yields,with a little algebra,
− d M v r e l = M d v . . . . ( 9 − 8 5 )
Dividing each side by d t gives us
− d t d M v r e l = M d t d v . . . . ( 9 − 8 6 )
We replace d M / d t (the rate at which the rocket loses mass) by − R ,where R is the (positive) mass rate of fuel consumption, and we recognize that d v / d t is the acceleration of the rocket.With these changes, Eq.9-86 becomes

Equation 9-87 holds for the values at any given instant. Note the left side of Eq. 9-87 has the dimensions of force ( k g / s ⋅ m / s = k g ⋅ m / s 2 = N ) and depends only on design characteristics of the rocket engine — namely, the rate R at which it consumes fuel mass and the speed v r e l with which that mass is ejected relative to the rocket. We call this term R v r e l the thrust of the rocket engine and represent it with T .Newton’s second law emerges clearly if we write Eq. 9-87 as T = M a , in which a is the acceleration of the rocket at the time that its mass is M .
Finding the Velocity
How will the velocity of a rocket change as it consumes its fuel? From Eq. 9-85 we have
− d M v r e l = M d v
Integrating leads to
∫ v i v f d v = − v r e l ∫ M i M f M d M ,
in which M i is the initial mass of the rocket and M f its final mass. Evaluating the integrals then gives
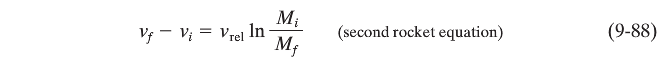
for the increase in the speed of the rocket during the change in mass from M i to M f . (The symbol “ln” in Eq. 9-88 means the natural logarithm.) We see here the advantage of multistage rockets, in which M f is reduced by discarding successive stages when their fuel is depleted. An ideal rocket would reach its destination with only its payload remaining.
See if you can apply this concept to the problem about barges. Have fun :)
Concept explanation credit: Fundamentals of Physics Extended, 9th Edition
Each minute 1000 kg of coal has to gain 10 km/h. Using SI measures, each second, 6 0 1 0 0 0 kg of coal has to gain 3 6 0 0 1 0 , 0 0 0 meters per second. Newton's second law F = m a tells us that the force to be applied to the coal is the product of these, 4 6 . 3 N .
Some notes: The acceleration occurs when the coals land in the target barge, so the work is done by (a). Because barge b gets lighter and barge (a) gets heavier, the friction of the water will increase on (a) and decrease on (b), so that the additional force needed to propell barge (b) will be negative, and that on (a) will be more than 46N. Their sum will remain the same, since nothing apart from the transferred coal undergoes an acceleration.
Consider the local exchange of momentum at each point in the shoveling process. When a shovelful of coal is lifted off the fast barge, the momentum imparted to the fast barge is only in the vertical direction. Since the shoveling doesn't change the momentum in the direction of motion, no force is required to keep the fast barge going at constant velocity. When it is put on to the slow barge, however, there is a change of momentum in the direction of motion, since the coal is moving at 10 km/hr relative to the slow barge.*
d t d p x = v d t d m = 1 0 h r k m ∗ 1 0 0 0 m i n k g = 2 . 8 s m ∗ 1 6 . 6 7 s k g = 4 6 N
By Newton's Law's, an equal and opposite force of 46 N is required to keep the slow barge moving at constant velocity. (As an aside- since all of the values stated in the problem only have one significant digit, 50 N would be a better answer.)
*Because 20 km/hr - 10 km/hr = 10 km/hr