Rod on a Hemisphere
A frictionless, hollow hemisphere of radius a centered at O is fixed so that its rim is in a horizontal plane. A smooth, uniform rod A B of mass m and length l is in equilibrium, with one end A resting on the inside of the hemisphere and the point C on the rod being in contact with the rim of the hemisphere. The rod is inclined at an angle of θ with the horizontal, as shown in the diagram.
What is the length of the rod l in terms of a ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The rod is static and thus there's neither net force nor net torque. From these conditions, we will derive relation between
l
and
a
(
x
is horizontal and
y
is vertical axis):
∑
X
=
0
⟹
F
C
sin
θ
=
F
A
cos
2
θ
∑
Y
=
0
⟹
F
C
cos
θ
+
F
A
sin
2
θ
=
G
∑
T
(
A
)
=
0
⟹
F
C
2
a
cos
θ
=
G
2
l
cos
θ
From the first two equations we get:
G
=
F
C
cos
2
θ
cos
θ
And plugging that into the third, one gets:
l
=
4
a
cos
θ
cos
2
θ
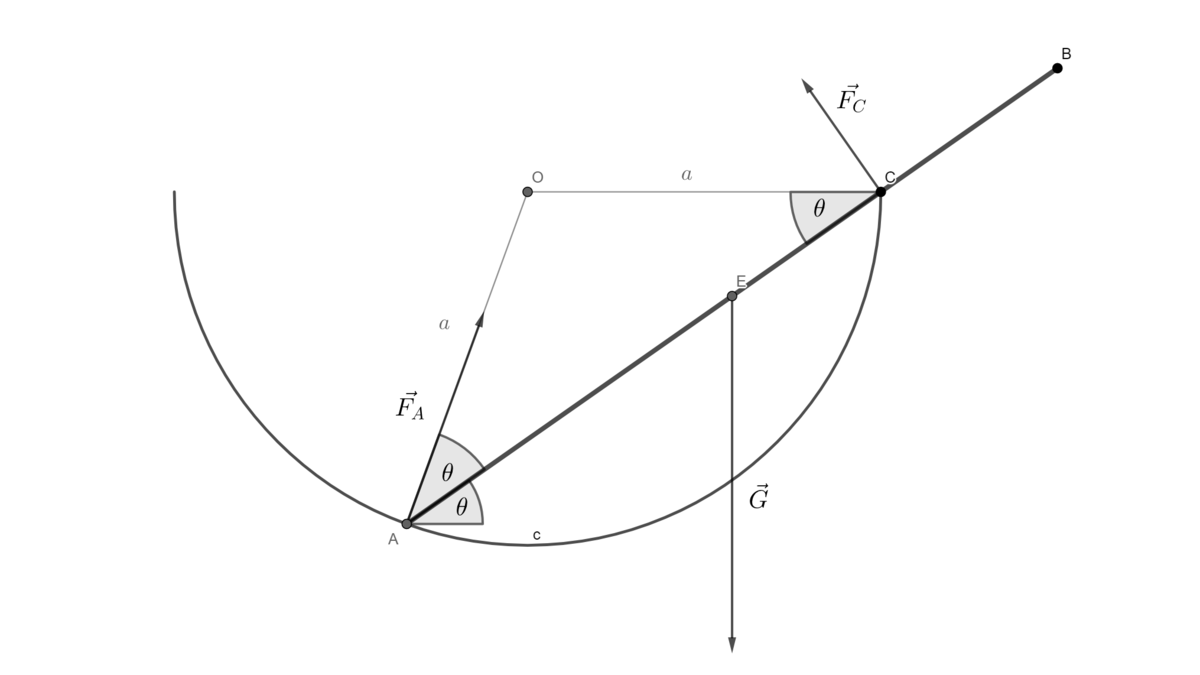 Point E is the center of mass of the rod
A more elegant way to solve this problem is to note that, in equilibrium, the center of mass of the rod is lowest possible. So, expressing the height of rod's center of mass as a function of
θ
and setting derivative to zero gives us desired condition:
h
∂
θ
∂
h
=
−
a
sin
2
θ
+
2
l
sin
θ
=
−
2
a
cos
2
θ
+
2
l
cos
θ
=
0
⟹
l
=
cos
θ
4
a
cos
2
θ
Point E is the center of mass of the rod
A more elegant way to solve this problem is to note that, in equilibrium, the center of mass of the rod is lowest possible. So, expressing the height of rod's center of mass as a function of
θ
and setting derivative to zero gives us desired condition:
h
∂
θ
∂
h
=
−
a
sin
2
θ
+
2
l
sin
θ
=
−
2
a
cos
2
θ
+
2
l
cos
θ
=
0
⟹
l
=
cos
θ
4
a
cos
2
θ
why can't we use law of cosines?
Resolving perpendicular to the rod, AB: S sin θ + R = m g cos θ
Resolving parallel to AB: S cos θ − m g sin θ = 0
⇒ S = cos θ m g sin θ
⇒ m g cos θ sin 2 θ + R = m g cos θ
⇒ R = m g cos θ − m g cos θ sin 2 θ
⇒ R = cos θ m g ( cos 2 θ − sin 2 θ ) = cos θ m g ( cos 2 θ )
⇒ R = cos θ m g cos 2 θ
Taking moments about A: 2 l ( m g cos θ ) = 2 a cos θ ⋅ R as R acts through C and length AC = 2 a cos θ
⇒ l = m g 4 a ⋅ R
⇒ l = cos θ 4 a cos 2 θ .