Rod sliding and falling
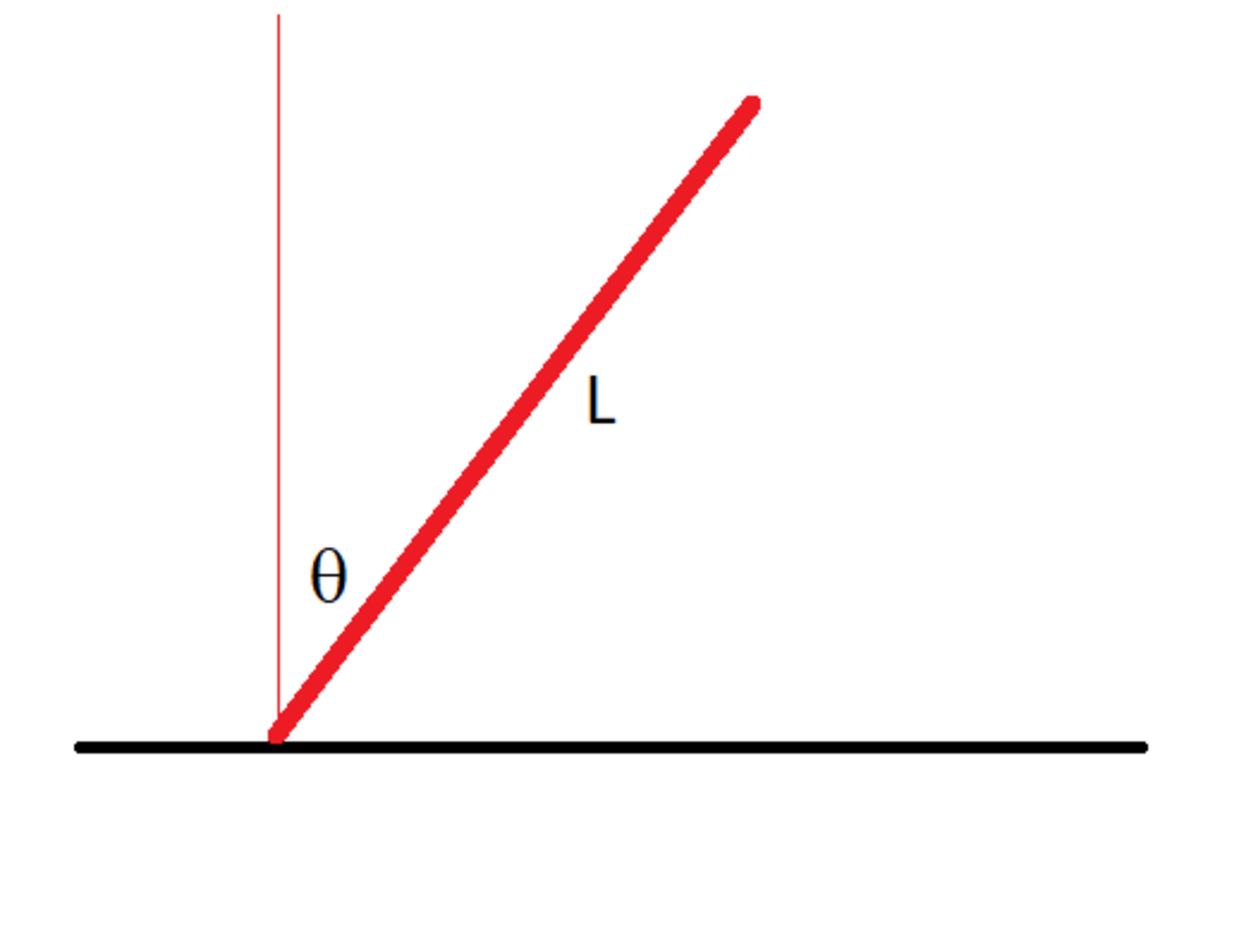
A rod of length L = 5 m is on a frictionless surface. Initially it is held vertical, then released with negligible initial velocity. The angle it makes with the vertical direction is θ as shown in the figure. Find the magnitude of the velocity of the upper tip of the rod when θ = 3 0 ∘ . Take g = 9 . 8 1 m / s 2 .
The answer is 4.44.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Karan Chatrath
very nice solution, upvoted.
BTW , I am also getting that same results for both cases, but don't know why.
Why to upload solution , if I know that you will not give any credit, even not a single upvote.
You don't care of those people who are doing hardwork in posting solution of your problem.
That's very wrong.
Think of uploading your solutions as a way of showing other people how to solve the problem. Then it does not matter if you get upvoted or not!
Log in to reply
@Mark Hennings But if someone put in the time of solving a problem of someone else's, it would be nice to at least have the courtesy of giving an upvote.
As a rule of thumb, I always upvote solutions to my problems. I think recognising every solution, no matter how presentable or clear it is, is important, given that someone put in a few minutes of their time to solve your problem.
However, I do believe that some people will get more recognition depending on the quality of the solution. But the person who posted the problem should have the courtesy of upvoting a solution. By the way, Neeraj did post quite a nice solution to the problem. There was no reason he didn't deserve an upvote.
I agree with your point, overall. Solutions should be posted; upvotes will come naturally.
@Krishna Karthik
now lets end this matter here only.
If Mark sir is saying something, he is saying right thing only.
Respect his words and move on.
I will upload solutions no matter if I gets upvote or not.
Log in to reply
I agree. You shouldn't focus on upvotes when posting a solution. In that regard, Mark Hennings is quite right. Btw, I agree with you on the fact that the poster of the problem should recognise the work of the solver.
You got very upset and mad at me, because I did not upvote one of your solutions. I don't think I have an obligation to upvote a solution if I don't find it worthy of an upvote. Many of my own solutions do not get upvoted at all, although to me they seem like very good solutions, but I understand that other members of Brilliant.com need not share the same view about them. If you post a good solution in a presentable and clear style, then I have no problem upvoting it.
Log in to reply
@Hosam Hajjir I agree; his anger was unwarranted for. However, when someone solves one of your own problems, I feel it's nice to give an upvote, because that person put in the time to write a solution and solve your problem. I agree with the fact that members are free to give an upvote to a solution they feel is worthy, but since it is your own problem that he took the time in solving, it would be courteous to give recognition to it.
Don't be a hypocrite Neeraj, you didn't upvote my detailed answer to your questions as well.
@Pi Han Goh
we have already ended this matter, but if you want to join, it is upto you.
Basically the upvote option of discussion are at the right side , which is very less visible than the upvote of a problem.
Think logically the upvote of a problem is directly below, so we can directly upvote it and there many options of upvoting like (Helpful, Interesting, Brilliant, Confused)
While the upvote of discussion doesn't contain this, and I am on a Brilliant website from last 8 months and posting discussion from last 2 months therefore I didn't have much experience of giving upvote in Discussion.
Besides this, I have said Thank you to you also, and also said your integration skill are good at that time only.
While if we talk about Hosam sir solution, he didn't give me upvote and also didn't said that “Thanks for solution”
“Nice alternative method” , even though my solution was different.
He didn't said
anything
.
But now I am following Mark sir, “post your solutions not for upvotes, but to show the method from which problem can be solved”
And here are some your solutions which I have upvoted countless times







Let the coordinates of the lowermost point on the rod be ( s , 0 ) . Then, the coordinates of the COM are:
x c = s + 2 L sin θ y c = 2 L cos θ
x ˙ c = s ˙ + 2 L cos θ θ ˙ y ˙ c = − 2 L sin θ θ ˙
The total kinetic energy of the rod is the sum of kinetic and rotational energy which is:
T = 2 m ( x ˙ c 2 + y ˙ c 2 ) + 2 1 ( 1 2 m L 2 ) θ ˙ 2
Potential energy:
V = 2 m g L cos θ
Applying momentum conservation along X gives:
x ˙ c = 0 ⟹ s ˙ = − 2 L cos θ θ ˙
Eliminating s ˙ in the kinetic energy expression gives:
T = 2 4 m L 2 θ ˙ 2 ( 4 − 3 cos 2 θ )
Applying conservation of energy gives and expression for θ ˙ 2 which is:
θ ˙ 2 = L 1 2 g ( 4 − 3 cos 2 θ 1 − cos θ )
Now, consider the upper tip of the rod. Its coordinates are:
x u = s + L sin θ y u = L cos θ
V 2 = x ˙ u 2 + y ˙ u 2 V 2 = 3 g L ( 1 − cos θ ) V ≈ 4 . 4 4
An interesting observation. If the lowermost point was hinged and the rigid rod rotates about the hinge from its initial vertical orientation, one sees that the expression for the speed of the uppermost tip is exactly the same as in this non hinged case. V 2 = 3 g L ( 1 − cos θ ) I wonder why this is so. Any insights would be appreciated.