Rods with Springs!
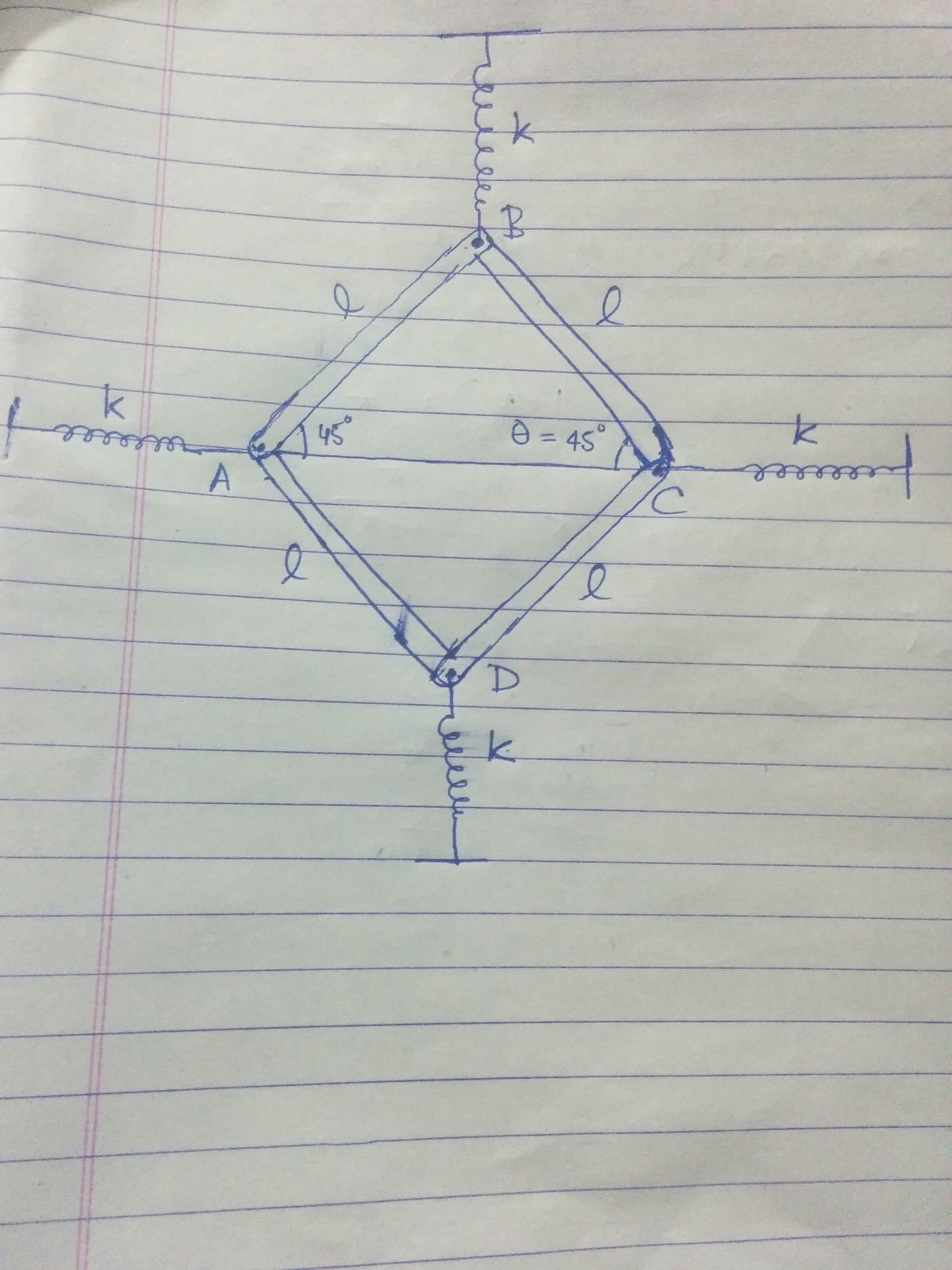
4 identical bars of mass and length are connected by pins at and . The bars are attached to four massless springs of same spring constant . The entire system can move in horizontal plane. In the equilibrium position as shown in figure. If the corners and are given a slight displacement away from each other and released, find angular frequency of small oscillations.
Details and Assumptions :
- There is no friction anywhere.
- .
- .
- .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Click here to view full image
Let the rods be rotated by a small angle θ so that they make an angle 4 5 ° − θ with A C It is easy to see that in this process the springs at A and C would be compressed by a = L ( cos ( 4 5 ° − θ ) − cos 4 5 ° ) and the springs at B and D would be extended by b = L ( sin 4 5 ° − sin ( 4 5 ° − θ ) ) . At this instant potential energy of the system could be written as
P E = ( 2 ∗ 2 1 K a 2 ) + ( 2 ∗ 2 1 K b 2 )
Plugging values of a and b and simplifying we get
P E = 2 K L 2 ( 1 − cos θ )
At this instant the rods are in pure rotation about their respective Instantenous centre of Rotation (IC)
Moment of inertia of each rod about respective IC
I = 1 2 M L 2 + M ( 2 L ) 2 = 3 M L 2 (parallel axis theorem)
The Kinetic Energy of the system at this instant would be
K E = 4 ∗ 0 . 5 ∗ I ω 2
Total Energy T E = P E + K E = c o n s t .
T E = 2 K L 2 ( 1 − cos θ ) + 2 ∗ I ω 2 = c o n s t .
Differentiating wrt. Time we get 2 K L 2 ( sin θ ) θ ˙ + 3 4 M L 2 ω ω ˙ = 0
As ω = θ ˙ a n d ω ˙ = θ ¨ on simplifying we get
K L 2 sin θ + ( 2 / 3 ) M L 2 θ ¨ = 0
On further simplification and using sin θ ≈ θ we get
θ ¨ = − 2 M 3 K θ
So Angular frequency = 2 M 3 K