Rolled Up Cylinder

Geometry Level 3

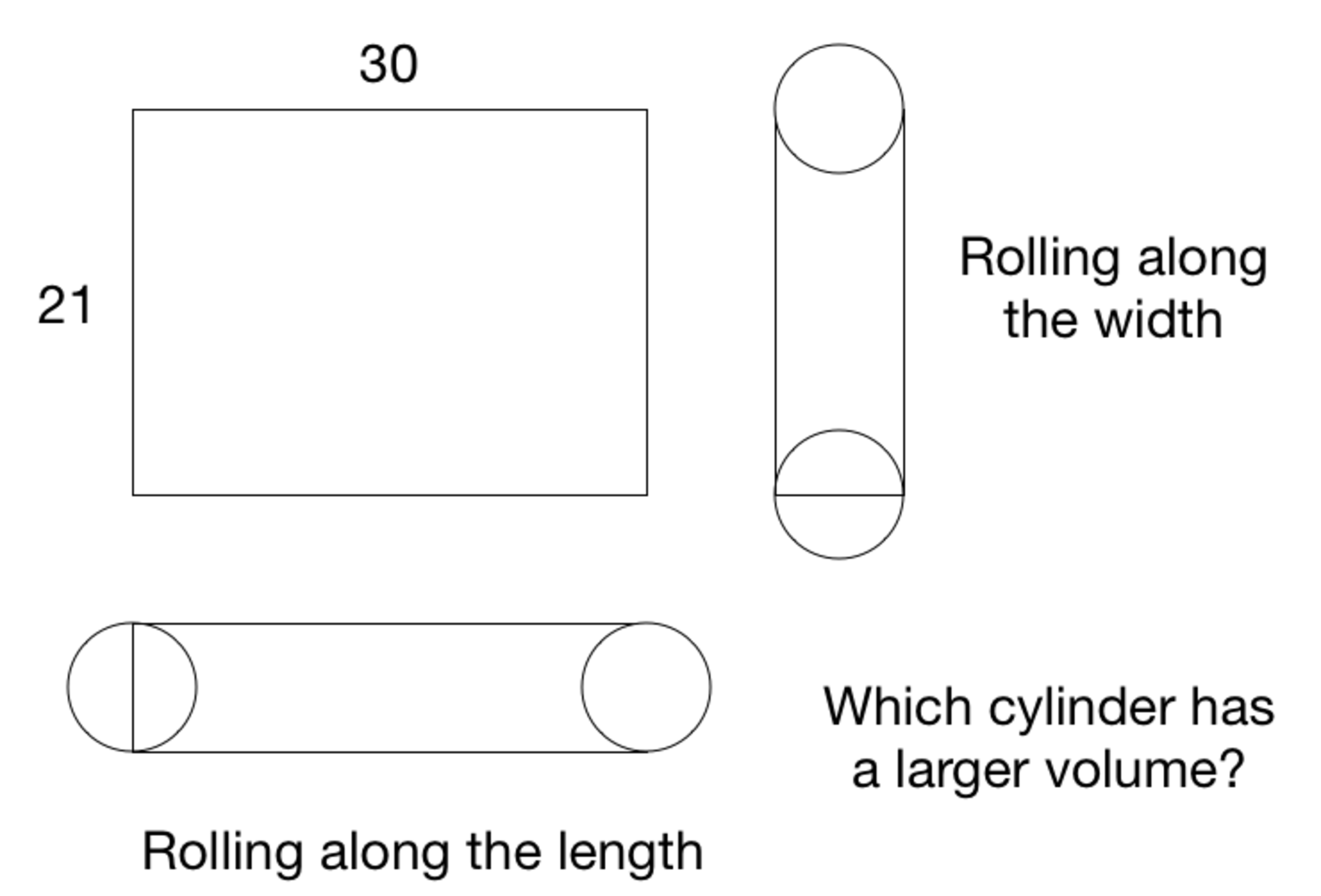
Suppose we have a piece of paper that measured 21 by 30, that we wanted to use to form a cylinder.
We can either roll it up along the width, or roll it up along the length, which forms the height of the cylinder.

Which cylinder would have a larger volume?

Rolling along the width Rolling along the length Equal volume

2 solutions

Michael Mendrin
Jan 6, 2017

The one that's closer to a sphere wins.

How do you know that?

Pi Han Goh - 4 years, 5 months ago

Suppose the rolled-up cylinders are like soap bubbles. Suppose we start with the long soap bubble. As it changes to eventually become a nice round sphere, it'll transition to a state more like the correct solution---along the way. Now scale the results so that the surface area is approximately constant.

Of course, basic volume algebra work will show this to be true anyway.

$\pi { \left( \dfrac{21}{2 \pi} \right) }^{2} 30=1052.81...$
$\pi { \left( \dfrac{30}{2 \pi} \right) }^{2} 21=1504.01...$

Michael Mendrin - 4 years, 5 months ago

Vishwash Kumar Γξω
Jan 14, 2017

Just pi r^2 h. Substitute the measures of cylinders on this formula.

Rolled Up Cylinder

2 solutions

0 pending reports