Roller coaster
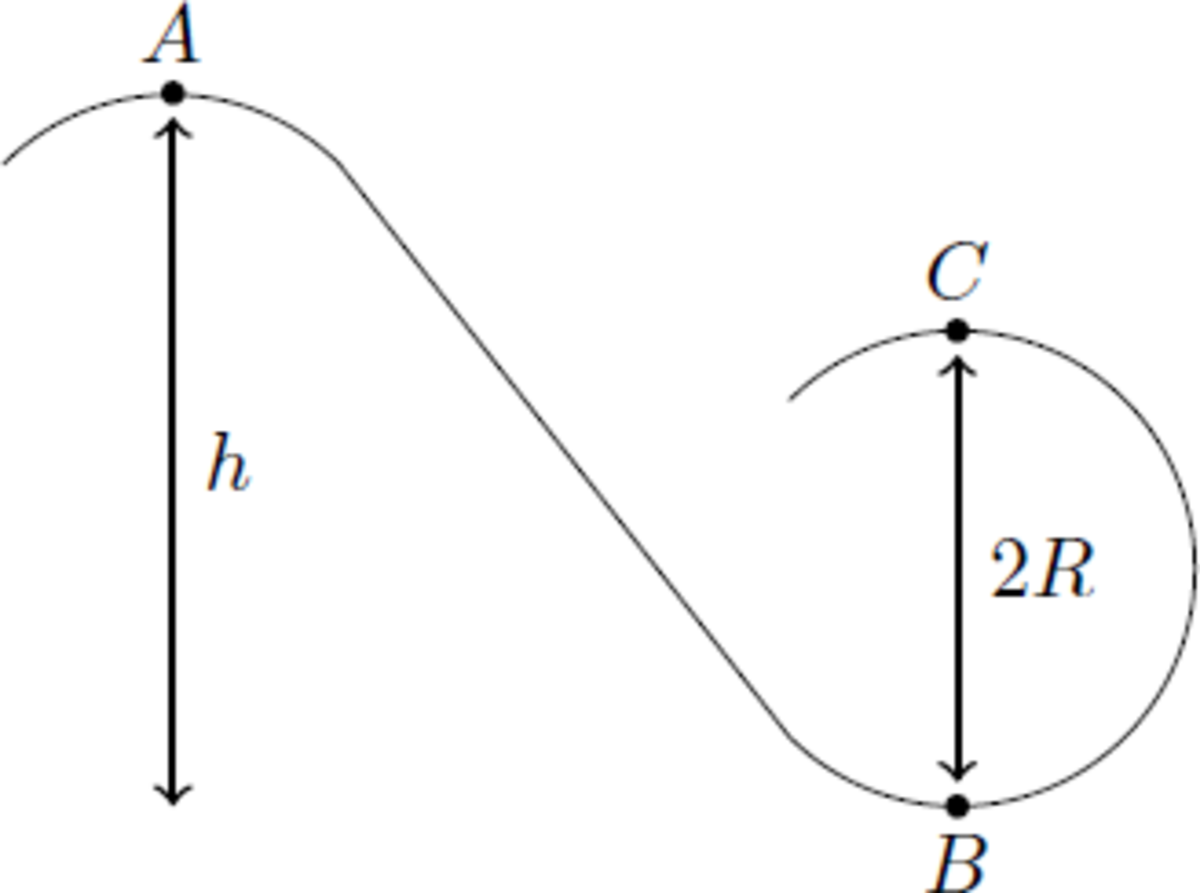
We consider a roller coaster with a lift hill of height h = 30 m and a circular looping with radius R = 10 m. We assume, that the cars are only accelerated by gravity. If the cars start with zero velocity at point A, how large are the absolute values of the g-force in point B and C?
Additional question: A vertical g-force up to 5g is for the human body easily bearable. Can you modify the roller coaster, so that the maximal g-force is below this value (without removing the looping)?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The total energy
E = U + T = m g y + 2 1 m v 2 (potential and kinetic energy)
of a car with height y , velocity v and mass m is conserved along the track. The energy in the points A, B and C reads:
E A E B E C = m g h = 2 1 m v B 2 = 2 1 m v C 2 + 2 m g R E A = E B ⇒ E A = E C ⇒ v B = 2 g h v C = 2 g ( h − 2 R )
With the help of the velocities v B and v C we can caculate the centrifugal force F cf = ± m v 2 / R inside the looping. With the gravitional force F g = − m g we get the total force, that acts on the passengers:
F B F C = − m R v B 2 − m g = − ( R 2 h + 1 ) m g = − 7 ⋅ m g = + m R v C 2 − m g = + ( R 2 h − 5 ) m g = + 1 ⋅ m g