Rolling a 35 with 10 Dice
If the probability that 1 0 regular 6 -sided dice add up to 3 5 is exactly q p , where p and q are coprime positive integers, then find p + q .
The answer is 112607.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Fantastic. Great method, thanks for sharing it.
This is multinomial theorem?
Log in to reply
No. I am simply using the standard Binomial Theorem and the Inverse Binomial Theorem. I could use the Multinomial Theorem to say that X = ( k 1 , k 2 , . . . . , k 6 ) ∈ K ∑ ( k 1 k 2 1 0 k 3 ⋯ k 6 ) where K = { ( k 1 , k 2 , . . . , k 6 ) ∈ ( N ∪ { 0 } ) 6 ∣ ∣ k 1 + k 2 + ⋯ + k 6 = 1 0 , k 1 + 2 k 2 + 3 k 3 + ⋯ 6 k 6 = 3 5 } but evaluating X that way would be hard work.
Log in to reply
I am yet to learn the inverse binomial theorem. Side question: Can you give examples of where the multinomial theorem is best at use. Thanks though!
It works with Windows:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
|
Output:
1 |
|
Solution:
6 1 0 4 3 9 5 4 5 6 = 1 0 4 9 7 6 7 6 3 1 ⟹ p + q = 7 6 3 1 + 1 0 4 9 7 6 = 1 1 2 6 0 7
I used the generating function method
g ( x ) = ( x + x 2 + x 3 + x 4 + x 5 + x 6 ) 1 0
You can convince yourself that the coefficient of x k in g ( x ) is exactly the number of ways to get a sum of k on the 1 0 dice.
I used simple code to find the coefficients of the resulting polynomial g ( x ) . The coefficient of x 3 5 is 4 3 9 5 4 5 6
Therefore, the probability is P = 6 1 0 4 3 9 5 4 5 6 = 1 0 4 9 7 6 7 6 3 1 in smallest terms.
And this makes the answer 7 6 3 1 + 1 0 4 9 7 6 = 1 1 2 6 0 7
I did this the same way but have a nagging suspicion there's a shortcut.
There is. Try my solution
Since code is used, I addressed directly as follows using the code environment available on this Brilliant website.
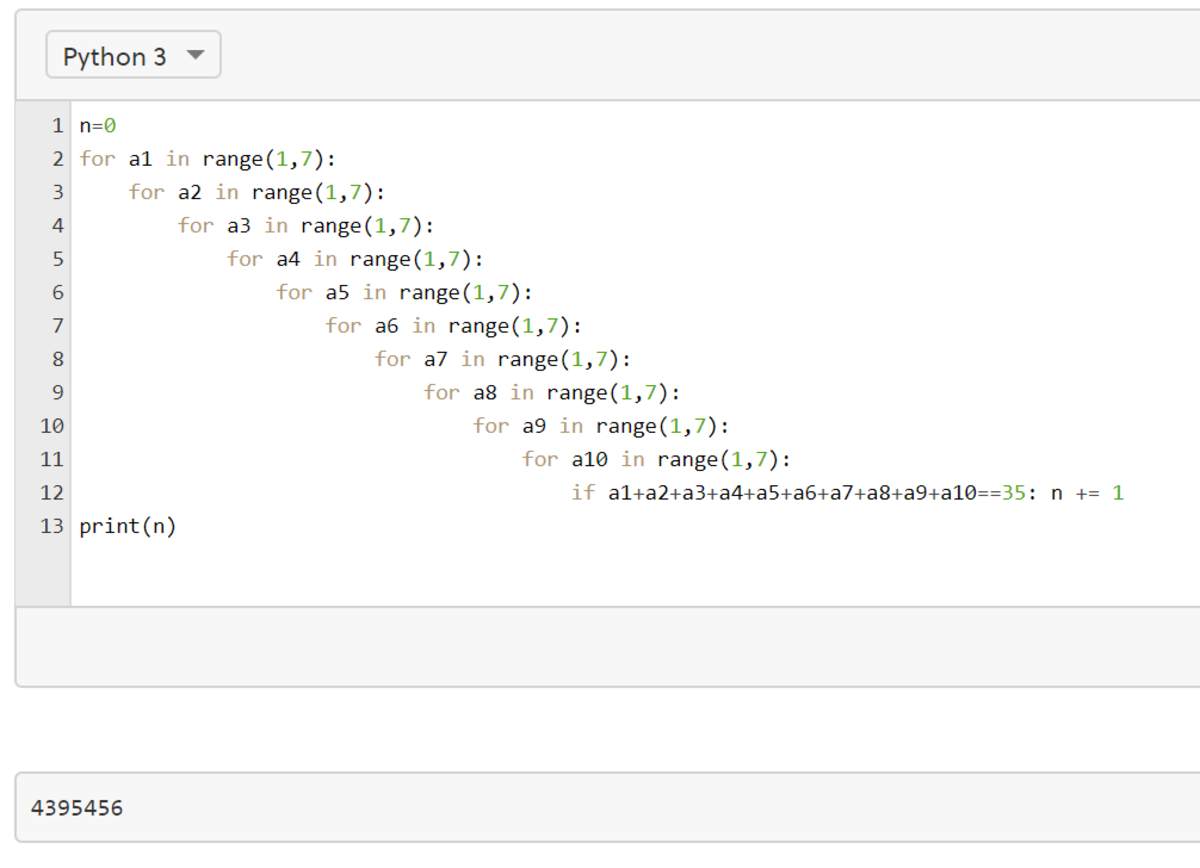
Then q p = 6 1 0 4 3 9 5 4 5 6 = 1 0 4 9 7 6 7 6 3 1 and p + q = 7 6 3 1 + 1 0 4 9 7 6 = 1 1 2 6 0 7 .
Why range(1,7) and not range(1,6) ?
Log in to reply
Python index is such. range(a,b) means from a to b-1.
range(a, b) creates integers between a and b - 1 inclusive.
Without code... We want the coefficient of x 3 5 in the series expansion of ( x + x 2 + x 3 + x 4 + x 5 + x 6 ) 1 0 = x 1 0 ( 1 − x 6 ) 1 0 ( 1 − x ) − 1 0 = x 1 0 ( m = 0 ∑ 1 0 ( − 1 ) m ( m 1 0 ) x 6 m ) ( n = 0 ∑ ∞ ( 9 9 + n ) x n ) = m = 0 ∑ 1 0 n = 0 ∑ ∞ ( − 1 ) m ( m 1 0 ) ( 9 9 + n ) x 1 0 + 6 m + n which is X = m = 0 ∑ 4 ( − 1 ) m ( m 1 0 ) ( 9 3 4 − 6 m ) = 4 3 9 5 4 5 6 making the probability equal to 6 1 0 X = 1 0 4 9 7 6 7 6 3 1 which gives the answer 7 6 3 1 + 1 0 4 9 7 6 = 1 1 2 6 0 7 .